Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
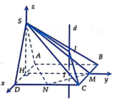
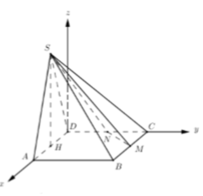
Gọi H là trung điểm của A D ⇒ S H ⊥ ( A B C D ) ⇒ S H = a 3
Cho hệ trục tọa độ như hình vẽ ⇒ D ( a ; 0 ; 0 ) , M ( 0 ; 2 a ; 0 ) , N ( a ; a ; 0 )
⇒ Trung điểm MN là I a 2 ; 3 a 2 ; 0 có S 0 ; 0 ; a 3 , C a ; 2 a ; 0
Gọi d là đường thẳng đi qua I và vuông góc với (ABCD)
⇒ d có vecto chỉ phương k → = 0 ; 0 ; 1
∆ N C M vuông tại C là tâm đường tròn ngoại tiếp
⇒ d là trục của đường tròn ngoại tiếp tam giác CMN
⇒ Tâm J của mặt cầu ngoại tiếp SCMN thuộc d
Ta có d qua I a 2 ; 3 a 2 ; 0 và k → = 0 ; 0 ; 1 là vecto chỉ phương ⇒ d : x = a 2 y = 3 a 2 z = t
⇒ J a 2 ; 3 a 2 ; t mà J C = J S ⇒ a 2 2 + a 2 2 + t 2 = a 2 2 + 3 a 2 2 + a 3 - t 2
⇒ t = 5 a 3 6 Bán kính R = J C = 93 6 a .

Đáp án C
Gọi O là trung điểm của SD. Ta có: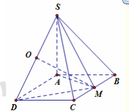
A D = D M = a 2 và A D = 2 a ⇒ A M ⊥ D M
Lại có D M ⊥ S A ⇒ D M ⊥ S A M ⇒ D M ⊥ S M
Vì tam giác SAD vuông tại A nên OS = OD = OA. Tương tự với tam giác SMD nên OS = OD = OM.
Vậy O là tâm mặt cầu ngoại tiếp hình chóp S.ADM. Khi đó R = S D 2 = S A 2 + D A 2 2 = a 6 2 .

Đáp án D
Phương pháp:
- Tìm một mặt phẳng chứa SK mà song song với MN, đó chính là mặt phẳng (SAD)
- Từ đó ta chỉ cần tính khoảng cách từ MN đến (SAD).
Cách giải: Gọi I là trung điểm AD, AC cắt BD tại O. H là hình chiếu vuông góc của O trên SI.
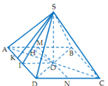
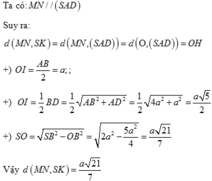
Chú ý khi giải: HS thường không chú ý đến phương pháp tìm mặt phẳng song song mà chỉ tập trung đi tìm đường vuông góc chung dẫn đến sự phức tạp cho bài toán và không đi đến được đáp án.

Giả sử C(c,3-c). Gọi I là giao điểm của AC và MN, suy ra \(\overrightarrow{AI}=\dfrac{2}{3}\overrightarrow{AC}=\left(\dfrac{2(c+2)}{3};\dfrac{2(3-c)}{3}\right)\)
Do đó \(I\left(\dfrac{2c-2}{3};\dfrac{6-2c}{3}\right)\in MN:7x-6y-5=0\Rightarrow c=\dfrac{5}{2}\). Vậy \(C\left(\dfrac{5}{2};\dfrac{1}{2}\right)\)
Trung điểm của AC là \(P\left(\dfrac{1}{4};\dfrac{1}{4}\right),\overrightarrow{AC}\left(\dfrac{7}{2};\dfrac{1}{2}\right)\Rightarrow B\left(\dfrac{1}{4}+t;\dfrac{1}{4}-7t\right), D\left(\dfrac{1}{4}-t;\dfrac{1}{4}+7t\right)\).
Vì \(BP=CP=\dfrac{AC}{2}=\dfrac{5\sqrt{2}}{2}\)nên \(t=\pm\dfrac{1}{2}\)
Vậy \(B\left(\dfrac{3}{4};-\dfrac{13}{4}\right),D\left(-\dfrac{1}{4};\dfrac{15}{4}\right)\)hoặc \(B\left(-\dfrac{1}{4};\dfrac{15}{4}\right),D\left(\dfrac{3}{4};-\dfrac{13}{4}\right)\).




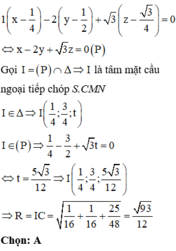


Chọn D