
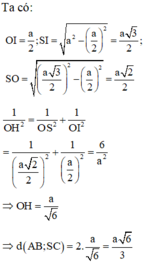
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


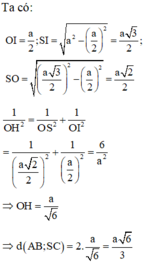

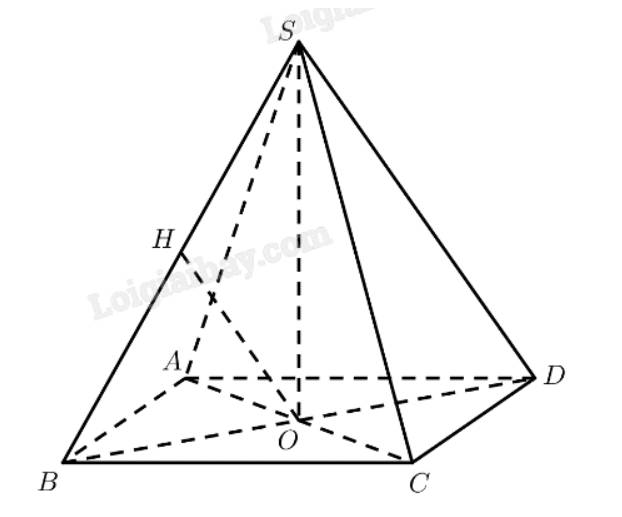
a) Kẻ \(OH \bot SB\left( {H \in SB} \right)\)
\(S.ABC{\rm{D}}\) là chóp tứ giác đều \( \Rightarrow SO \bot \left( {ABCD} \right) \Rightarrow SO \bot AC\)
\(ABC{\rm{D}}\) là hình vuông \( \Rightarrow AC \bot B{\rm{D}}\)
\( \Rightarrow AC \bot \left( {SB{\rm{D}}} \right) \Rightarrow AC \bot OH\)
Mà \(OH \bot SB\)
\( \Rightarrow d\left( {AC,SB} \right) = OH\)
\(B{\rm{D}} = \sqrt {A{B^2} + A{{\rm{D}}^2}} = a\sqrt 2 \Rightarrow BO = \frac{1}{2}B{\rm{D}} = \frac{{a\sqrt 2 }}{2}\)
\(\Delta SBO\) vuông tại \(O \Rightarrow SO = \sqrt {S{B^2} - B{O^2}} = \frac{{a\sqrt 2 }}{2}\)
\(\Delta SBO\) vuông cân tại \(O\) có đường cao \(OH\)
\( \Rightarrow d\left( {AC,SB} \right) = OH = \frac{1}{2}SB = \frac{a}{2}\)
b) \({S_{ABC{\rm{D}}}} = A{B^2} = {a^2}\)
\({V_{S.ABC{\rm{D}}}} = \frac{1}{3}{S_{ABC{\rm{D}}}}.SO = \frac{{{a^3}\sqrt 2 }}{6}\)

\(\left\{{}\begin{matrix}BD\perp SO\\BD\perp AC\end{matrix}\right.\) \(\Rightarrow BD\perp\left(SAC\right)\)
Từ O kẻ \(OH\perp SA\) (H thuộc SA)
Do \(OH\in\left(SAC\right)\Rightarrow BD\perp OH\)
\(\Rightarrow OH\) là đường vuông góc chung BD và SA hay \(OH=d\left(BD;SA\right)\)
\(AC=a\sqrt{2}\Rightarrow AO=\dfrac{1}{2}AC=\dfrac{a\sqrt{2}}{2}\) ; \(SO=\sqrt{SA^2-AO^2}=\dfrac{a\sqrt{2}}{2}\)
\(\Rightarrow\Delta SAO\) vuông cân tại O
\(\Rightarrow OH=\dfrac{1}{2}SA=\dfrac{a}{2}\)

Gọi O là tâm đáy \(\Rightarrow SO\perp\left(ABCD\right)\Rightarrow\widehat{SCO}\) là góc giữa SC và (ABCD) hay \(\widehat{SCA}\) là góc giữa SC và (ABCD) (do A,C,O thẳng hàng)
\(AC=AB\sqrt{2}=a\sqrt{2}\)
\(\Leftrightarrow SA^2+SC^2=AC^2\Rightarrow\Delta SAC\) vuông cân tại S
\(\Rightarrow\widehat{SCA=45^0}\)

Đáp án D.
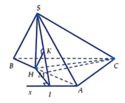
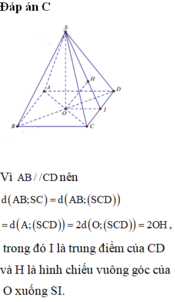
Kẻ Ax//BC, HI ⊥ Ax; HK ⊥ SI.
Gọi M là trung điểm của AB
![]()
![]()
Ta có AI ⊥ (SHI)=> AI ⊥ HK=> HK ⊥ (SAI)=>d(H,(Sax)) = HK
Góc giữa SC và (ABC) là góc S C H ^ = 60 0
Ta có:
![]()
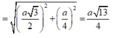
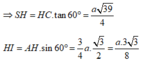
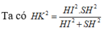
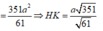
![]()
![]()

Gọi M là trung điểm của AD. Suy ra SM vuông góc mặt phẳng (ABCD).
a, Vì tam giác SAD là tam giác vuông cân
\(\Rightarrow SA=SD=\dfrac{a}{\sqrt{2}}=\dfrac{\sqrt{2}}{2}a\)
\(\Rightarrow SM=\sqrt{SA^2-AM^2}=\dfrac{1}{2}a\)
\(\Rightarrow V_{S.ABCD}=SM.S_{ABCD}=\dfrac{1}{2}a.a^2=\dfrac{1}{2}a^3\)
b, Qua M dựng đường thẳng MN song song với AB cắt BC tại N. Dựng MH vuông góc với SN.
Dễ dàng nhận thấy BC vuông góc với (SMN) do \(SM\perp BC;MN\perp BC\)
\(\Rightarrow MH\perp BC\)
mà \(MH\perp SN\Rightarrow MH\perp\left(SBC\right)\Rightarrow MH\perp SC\)
Hay MH chính là khoảng cách giữa AD và SC (Do cùng vuông góc)
Ta có: \(\dfrac{1}{MH^2}=\dfrac{1}{SM^2}+\dfrac{1}{MN^2}\Rightarrow\dfrac{1}{MH^2}=\dfrac{1}{\dfrac{1}{4}a^2}+\dfrac{1}{a^2}=\dfrac{5}{a^2}\Rightarrow MH=\dfrac{\sqrt{5}}{5}a\)