Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B.
Lời giải.
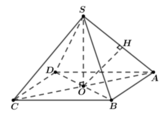
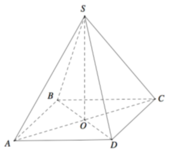
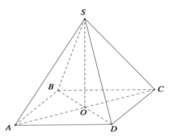
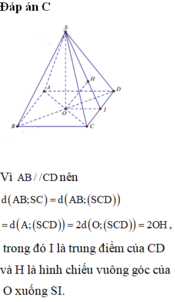
Xét hình chóp tứ giác đều S.ABCD, đặt AB =x, SO =h. Với O là tâm của hình vuông ABCD ⇒ S O ⊥ ( A B C D ) . Qua O kẻ đường thẳng OH vuông góc với SA với H ∈ SA
Ta có
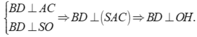
Suy ra OH là đoạn vuông góc chung của SA và BD
Theo bài ra, ta có
![]()
Tam giác SAO vuông tại O, có đường cao OH suy ra
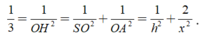
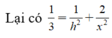
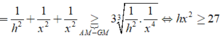
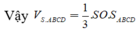
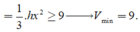

Do S.ABCD là chóp tứ giác đều \(\Rightarrow SH\perp\left(ABCD\right)\Rightarrow SH\perp AC\)
Mà \(AC\perp BD\) (hai đường chéo hình vuông)
\(\Rightarrow AC\perp\left(SBD\right)\Rightarrow\left(SAC\right)\perp\left(SBD\right)\)
b. Qua B kẻ đường thẳng song song AC cắt DC kéo dài tại E
\(\Rightarrow AC||\left(SBE\right)\Rightarrow d\left(AC;SB\right)=d\left(AC;\left(SBE\right)\right)=d\left(H;\left(SBE\right)\right)\)
\(\left\{{}\begin{matrix}AC\perp\left(SBD\right)\\AC||BE\end{matrix}\right.\) \(\Rightarrow BE\perp\left(SBD\right)\)
Trong tam giác vuông SBH, từ H kẻ \(HK\perp SB\Rightarrow HK\perp\left(SBE\right)\)
\(\Rightarrow HK=d\left(H;SBE\right)\)
\(BD=a\sqrt{2}\Rightarrow BH=\dfrac{BD}{2}=\dfrac{a\sqrt{2}}{2}\)
\(SH=\sqrt{SB^2-BH^2}=\dfrac{a\sqrt{3}}{2}\)
ÁP dụng hệ thức lượng:
\(HK.SB=SH.BH\Rightarrow HK=\dfrac{SH.BH}{SB}=\dfrac{a\sqrt{30}}{10}\)

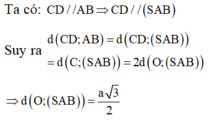


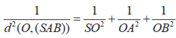
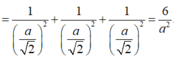
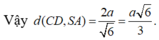

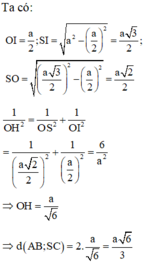
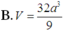
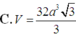
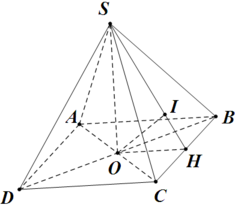
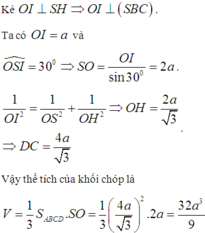
a) Kẻ \(OH \bot SB\left( {H \in SB} \right)\)
\(S.ABC{\rm{D}}\) là chóp tứ giác đều \( \Rightarrow SO \bot \left( {ABCD} \right) \Rightarrow SO \bot AC\)
\(ABC{\rm{D}}\) là hình vuông \( \Rightarrow AC \bot B{\rm{D}}\)
\( \Rightarrow AC \bot \left( {SB{\rm{D}}} \right) \Rightarrow AC \bot OH\)
Mà \(OH \bot SB\)
\( \Rightarrow d\left( {AC,SB} \right) = OH\)
\(B{\rm{D}} = \sqrt {A{B^2} + A{{\rm{D}}^2}} = a\sqrt 2 \Rightarrow BO = \frac{1}{2}B{\rm{D}} = \frac{{a\sqrt 2 }}{2}\)
\(\Delta SBO\) vuông tại \(O \Rightarrow SO = \sqrt {S{B^2} - B{O^2}} = \frac{{a\sqrt 2 }}{2}\)
\(\Delta SBO\) vuông cân tại \(O\) có đường cao \(OH\)
\( \Rightarrow d\left( {AC,SB} \right) = OH = \frac{1}{2}SB = \frac{a}{2}\)
b) \({S_{ABC{\rm{D}}}} = A{B^2} = {a^2}\)
\({V_{S.ABC{\rm{D}}}} = \frac{1}{3}{S_{ABC{\rm{D}}}}.SO = \frac{{{a^3}\sqrt 2 }}{6}\)