Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
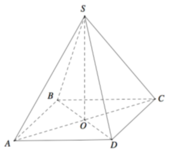
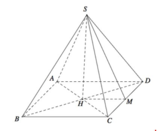
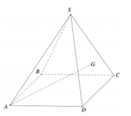
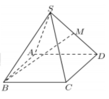
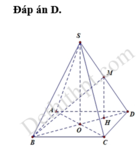
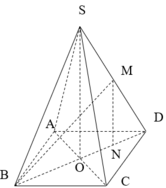
Gọi O là tâm hình vuông ABCD và M là trung điểm CD có S O = a 2 2 và H là hình chiếu vuông góc của G lên mặt phẳng (ABCD).
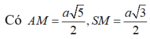
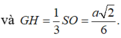
Vì
![]()
![]()
![]()
Và
![]()
![]()
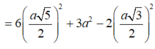
![]()
Vì vậy
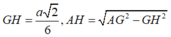
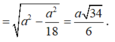
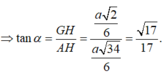

\(\left\{{}\begin{matrix}BD\perp SO\\BD\perp AC\end{matrix}\right.\) \(\Rightarrow BD\perp\left(SAC\right)\)
Từ O kẻ \(OH\perp SA\) (H thuộc SA)
Do \(OH\in\left(SAC\right)\Rightarrow BD\perp OH\)
\(\Rightarrow OH\) là đường vuông góc chung BD và SA hay \(OH=d\left(BD;SA\right)\)
\(AC=a\sqrt{2}\Rightarrow AO=\dfrac{1}{2}AC=\dfrac{a\sqrt{2}}{2}\) ; \(SO=\sqrt{SA^2-AO^2}=\dfrac{a\sqrt{2}}{2}\)
\(\Rightarrow\Delta SAO\) vuông cân tại O
\(\Rightarrow OH=\dfrac{1}{2}SA=\dfrac{a}{2}\)

Chọn C
Để cho gọn ta chọn a=2
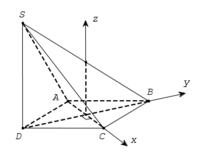
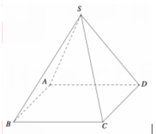
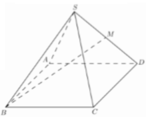
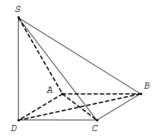
Chọn hệ trục tọa độ Oxyz như hình vẽ với O(0;0;0) và C(1;0;0), B(0; 3 ;0) S(0; - 3 ; x) với x =SD>0
Suy ra A(-1;0;0) và D(0;- 3 ;0)
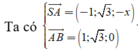
VTPT của mặt phẳng (SAB) là
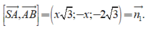
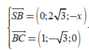
VTPT của mặt phẳng (SBC) là
![]()
Từ giả thiết bài toán, ta có
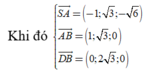
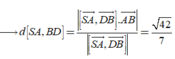
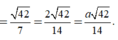
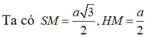
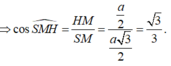

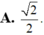

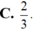
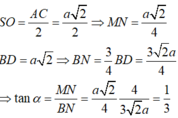
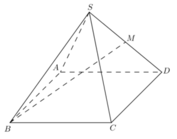
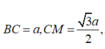
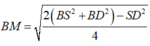
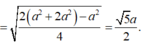
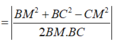
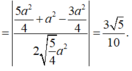
Đáp án D
Mặt khác S.OAB là tứ diện vuông đỉnh O nên