Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta tính được \(AG=a\dfrac{\sqrt{3}}{3}\)
Từ gt ta có:
\(\widehat{\left(SA,\left(ABC\right)\right)}=\widehat{\left(SA,AG\right)}=\widehat{SAG}=60^0\)(Vì S.ABC là chóp tam giác đều nên \(SG\perp\left(ABC\right)\))
Khi đó SG=AG.tan60=a
Gọi M là trung điểm BC \(\Rightarrow GM=a\dfrac{\sqrt{3}}{6}\)
Đặt d(G,(SBC))=x
Áp dụng mô hình "điểm tốt - vẽ hai bước" cho hình chóp S.GBC với G là "điểm tốt" ta có:
\(\dfrac{1}{x^2}=\dfrac{1}{SG^2}+\dfrac{1}{GM^2}=\dfrac{1}{a^2}+\dfrac{1}{\left(a\dfrac{\sqrt{3}}{6}\right)^2}\)
\(\Rightarrow x=\dfrac{a}{\sqrt{13}}\)
Mô hình "điểm tốt - vẽ hai bước": Cho hình chóp S.ABC với \(SA\perp\left(ABC\right)\). Kẻ \(AH\perp BC,AK\perp SH\) thì d(A,(SBC))=AK.
CM: Ta có: \(SA\perp\left(ABC\right)\Rightarrow SA\perp AH\)
Mà \(AH\perp BC\Rightarrow BC\perp\left(SAH\right)\)
\(\Rightarrow\left(SBC\right)\perp\left(SAH\right)\) theo giao tuyến SH
Mà \(AK\perp SH,AK\subset\left(SAH\right)\) \(\Rightarrow AK\perp\left(SBC\right)\), dễ dàng suy ra đpcm

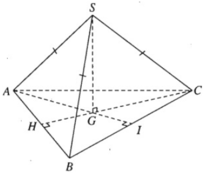
a) SG là trục đường tròn ngoại tiếp tam giác đều ABC nên SG ⊥ (ABC). Ta có
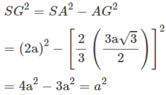
Vậy khoảng cách từ S tới mặt phẳng (ABC) là độ dài của đoạn SG = a
Ta có CG ⊥ AB tại H. Vì GH là đoạn vuông góc chung của AB và SG, do đó
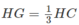
mà 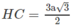
nên 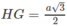

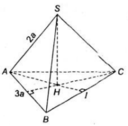
Gọi H là tâm của tam giác ABC ( khi đó H là trọng tâm, trực tâm của tam giác ABC).
Do hình chóp S.ABC là hình chóp tam giác đều nên SH ⊥ (ABC)

Vậy khoảng cách từ S đến (ABC ) là a.

Gọi H là tâm của tam giác ABC ( khi đó H là trọng tâm, trực tâm của tam giác ABC).
Do hình chóp S.ABC là hình chóp tam giác đều nên SH ⊥ (ABC)
\(AN=\sqrt{AB^2-BN^2}\) \(=\) \(\sqrt{\left(3a\right)^2-\left(\dfrac{3a}{2}\right)^2}\) \(=\) \(\dfrac{3a\sqrt{3}}{2}\)
Vậy khoảng cách từ S đến (ABC ) là a.

Chắc là tam giác SAB nằm trong mp vuông góc với đáy?
Gọi H là trung điểm AB \(\Rightarrow SH\perp AB\Rightarrow SH\perp\left(SAB\right)\)
\(\Rightarrow SH=d\left(S;\left(ABC\right)\right)\)
\(SH=\dfrac{AB\sqrt{3}}{2}=a\sqrt{3}\)

Chọn C.
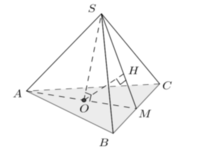
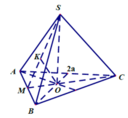
- Gọi O là trọng tâm của tam giác ABC và M là trung điểm của BC.
- Vì hình chóp S.ABC là hình chóp tam giác đều nên: S) ⊥ (ABC); SO = a√3.
- Kẻ OH ⊥ SM, ta có:
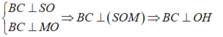 nên suy ra d(O; (SBC)) = OH.
nên suy ra d(O; (SBC)) = OH.
- Ta có:
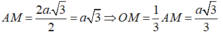
- Xét tam giác vuông SOM, đường cao OH có:
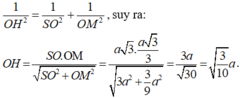




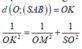
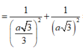
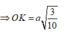
ĐÁP ÁN: D