Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

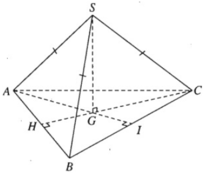
a) SG là trục đường tròn ngoại tiếp tam giác đều ABC nên SG ⊥ (ABC). Ta có
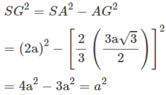
Vậy khoảng cách từ S tới mặt phẳng (ABC) là độ dài của đoạn SG = a
Ta có CG ⊥ AB tại H. Vì GH là đoạn vuông góc chung của AB và SG, do đó
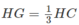
mà 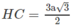
nên 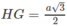

Chọn đáp án B
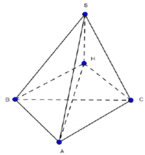
Gọi là H hình chiếu của đỉnh S xuống mặt phẳng (ABC). Khi đó, ta có
![]()
Ta có
![]()
Tương tự, ta cũng chứng minh được
![]()
Từ đó suy ra
![]()
Do SH ⊥ AB, BH ⊥ AB nên suy ra góc giữa (SAB) và (ABC) là góc SBH. Vậy SBH = 60 0
![]()
Trong tam giác vuông ABH, ta có
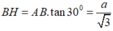
Trong tam giác vuông SHB, ta có
![]()
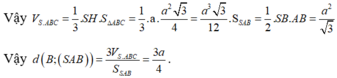

Chọn A

Gọi H là trung điểm của AC. Đỉnh S cách đều các điểm A, B, C
=> SH ⊥ (ABC)
Xác đinh được
![]()
Ta có MH // SA
![]()
Gọi I là trung điểm của AB => HI ⊥ AB
![]()
và chứng minh được HK ⊥ (SAB)
![]()
Trong tam giác vuông SHI tính được
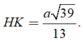

Đáp án B.
Gọi H là trung điểm AB, G là trọng tâm tam giác ABC, K là trung điểm SC.
Ta có: ![]()
SH = SC => HK là trung trực SC. Qua O kẻ trục d//SH => d ⊥ (ABC)
Gọi
![]()
=> I là tâm mặt cầu ngoại tiếp hình chóp SABC
Ta có
![]()
Xét ∆ HIG vuông tại G:
![]()
Vậy thể tích khối cầu ngoại tiếp hình chóp
![]()

Đáp án A
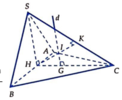
SM = M B tan 60 0 = 3 6
IG = x ⇒ JM = IG ⇒ SI = 1 12 + ( 3 6 + x ) 2 , IA = 1 3 + x 2
SI = IA ⇒ x 2 + 1 4 = ( x 2 + 3 3 x + 1 2 ) ⇒ x = 1 2 3 ⇒ R = 5 12
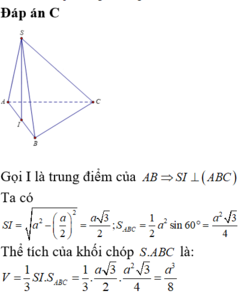
V = 4 3 πR 3 = 5 15 π 54

Chọn C.
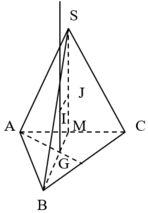
Gọi H là trung điểm của BC, suy ra .
![]()
Gọi K là trung điểm AC
![]()
![]()
![]()
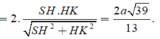

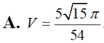
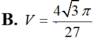
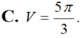
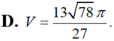

Chắc là tam giác SAB nằm trong mp vuông góc với đáy?
Gọi H là trung điểm AB \(\Rightarrow SH\perp AB\Rightarrow SH\perp\left(SAB\right)\)
\(\Rightarrow SH=d\left(S;\left(ABC\right)\right)\)
\(SH=\dfrac{AB\sqrt{3}}{2}=a\sqrt{3}\)