Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D
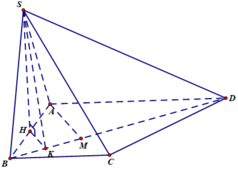
Ta có ![]()
Gọi H là trung điểm AB thì ![]() ,
,
kẻ ![]() , ta có
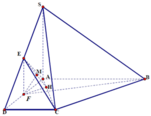
, ta có ![]() là góc giữa (SBD) và (ABCD), do đó
là góc giữa (SBD) và (ABCD), do đó ![]() = 600
= 600
Gọi AM là đường cao của tam giác vuông ABD. Khi đó, ta có:
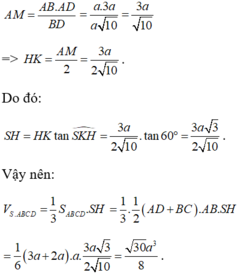

Gọi H là trung điểm của AB, suy ra \(SH\perp\left(ACBD\right)\)
Do đó \(SH\perp HD\) ta có :
\(SH=\sqrt{SD^2-DH^2}=\sqrt{SD^2-\left(AH^2+AD^2\right)}=a\)
Suy ra \(V_{s.ABCD}=\frac{1}{3}.SH.S_{ABCD}=\frac{a^2}{3}\)
Gọi K là hình chiếu vuông góc của H trên BD và E là hình chiếu vuông góc của H lên SK. Ta có :
\(\begin{cases}BD\perp HK\\BD\perp SH\end{cases}\) \(\Rightarrow BH\perp\) (SHK)
=> \(BD\perp HE\) mà \(HE\perp SK\) \(\Rightarrow HE\perp\) (SBD)
Ta có : HK=HB.\(\sin\widehat{KBH}\)\(=\frac{a\sqrt{2}}{4}\)
Suy ra \(HE=\frac{HS.HK}{\sqrt{HS^2+HK^2}}=\frac{a}{3}\)
Do đó \(d\left(A:\left(SBD\right)\right)\)=2d(H; (SBD)) =3HE=\(\frac{2a}{3}\)
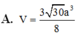
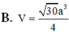
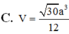
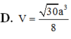
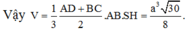


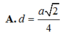
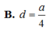
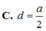
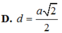

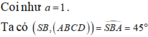


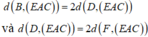
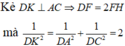

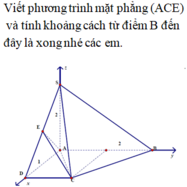

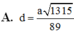
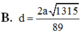
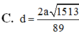
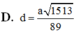

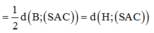

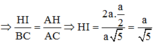
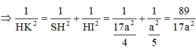
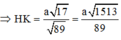
Phương pháp:
Xác định chiều cao hình chóp bằng kiến thức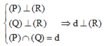
Xác định khoảng cách
Tính toán bằng cách sử dụng quan hệ diện tích, định lý hàm số cosin, công thức tính diện tích tam giác S = 1 2 a.h với a là cạnh đáy, h là chiều cao tương ứng và
Cách giải:
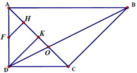
Gọi H = AM ∪ BD
Ta có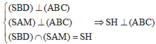
Vì AB//CD nên theo định lý Ta-lét ta có
Ta có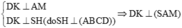
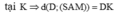
Vì M là trung điểm của DC và ABCD là hình bình hành có diện tích 2 a 2 nên ta có:
Lại có CD = AB = a 2
Khi đó

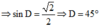
Lại có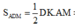
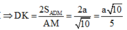
Từ đó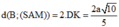
Chọn: C