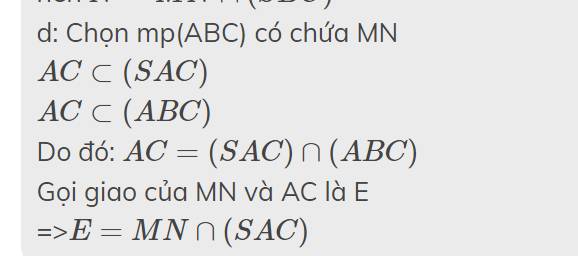Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu b đề sai, hai mặt phẳng (SAC) và (SBD) không hề vuông góc với nhau (chúng chỉ vuông góc trong trường hợp ABCD là hình vuông)
Do câu b đề sai, (SAC) và (SBD) không vuông góc nên câu c rất khó tính :(
Từ A, kẻ \(AH\perp\left(SBD\right)\)
Gọi K là điểm đối xứng H qua O \(\Rightarrow\) AHCK là hình bình hành (tứ giác có 2 đường chéo cắt nhau tại trung điểm)
\(\Rightarrow\left\{{}\begin{matrix}CK//AH\\CK=AH\end{matrix}\right.\Rightarrow CK\perp\left(SBD\right)\) (K đương nhiên thuộc (SBD) do H, O đều thuộc (SBD))
\(\Rightarrow\widehat{CSK}\) là góc cần tìm
Trong mp (SBD), nối B và H kéo dài cắt SD tại E
\(\left\{{}\begin{matrix}SA\perp AB\\AB\perp AD\end{matrix}\right.\) \(\Rightarrow AB\perp\left(SAD\right)\Rightarrow AB\perp SD\) (1)
Mà \(AH\perp\left(SBD\right)\Rightarrow AH\perp SD\) (2)
(1);(2) \(\Rightarrow SD\perp\left(ABE\right)\Rightarrow SD\perp AE\)
Áp dụng hệ thức lượng trong tam giác vuông SAD:
\(\frac{1}{AE^2}=\frac{1}{SA^2}+\frac{1}{AD^2}\)
Áp dụng hệ thức lượng trong tam giác vuông ABE:
\(\frac{1}{AH^2}=\frac{1}{AB^2}+\frac{1}{AE^2}=\frac{1}{AB^2}+\frac{1}{SA^2}+\frac{1}{AD^2}=\frac{1}{a^2}+\frac{1}{9a^2}+\frac{1}{4a^2}\Rightarrow AH=\frac{6a}{7}\)
Số đẹp quá ta :D
\(\Rightarrow CK=\frac{6a}{7}\)
Lại có:
\(SC=\sqrt{SA^2+AC^2}=\sqrt{SA^2+AB^2+BC^2}=a\sqrt{14}\)
\(\Rightarrow sin\widehat{CSK}=\frac{CK}{SC}=\frac{6}{7\sqrt{14}}\)

\(SA\) là giao tuyến của (SAB) và (SAD)
Mà (SAB) và (SAD) cùng vuông góc (ABCD)
\(\Rightarrow SA\perp\left(ABCD\right)\)
b/\(SA\in\left(SAC\right)\Rightarrow\left(SAC\right)\perp\left(ABCD\right)\)
c/ \(SA\perp\left(ABCD\right)\Rightarrow\widehat{SDA}\) là góc giữa SD và (ABCD)
\(tan\widehat{SDA}=\frac{SA}{AD}=\frac{a\sqrt{6}}{2a}=\frac{\sqrt{6}}{2}\Rightarrow\widehat{SDA}\approx50^046'\)
\(AC=\sqrt{AB^2+BC^2}=a\sqrt{2}\)
Gọi M là trung điểm AD \(\Rightarrow DM=a\Rightarrow CD=\sqrt{DM^2+CM^2}=a\sqrt{2}\)
\(\Rightarrow AC^2+CD^2=AD^2\Rightarrow CD\perp AC\)
Mà \(SA\perp\left(ABCD\right)\Rightarrow SA\perp CD\)
\(\Rightarrow CD\perp\left(SAC\right)\)
Lại có CD là giao tuyến của (ABCD) và (SCD)
\(\Rightarrow\widehat{SCA}\) là góc giữa (ABCD) và (SCD)
\(tan\widehat{SCA}=\frac{SA}{AC}=\frac{a\sqrt{6}}{a\sqrt{2}}=\sqrt{3}\Rightarrow\widehat{SCA}=60^0\)

1:
a: \(S\in SA\)
\(S\in SB\subset\left(SBC\right)\)
Do đó: \(S=SA\cap\left(SBC\right)\)
b: Chọn mp(SAB) có chứa SM
\(AB\subset\left(ABC\right)\)
\(AB\subset\left(SAB\right)\)
Do đó: \(AB=\left(SAB\right)\cap\left(ABC\right)\)
\(M\in AB\)
=>SM giao AB=M
=>\(M=SM\cap\left(ABC\right)\)
c: Chọn mp(BAC) có chứa MN
\(BC\subset\left(BAC\right)\)
\(BC\subset\left(SBC\right)\)
Do đó: (BAC) giao (SBC)=BC
mà \(BC\cap MN=N\)
nên \(N=MN\cap\left(SBC\right)\)
d: Chọn mp(ABC) có chứa MN
\(AC\subset\left(SAC\right)\)
\(AC\subset\left(ABC\right)\)
Do đó: \(AC=\left(SAC\right)\cap\left(ABC\right)\)
Gọi giao của MN và AC là E
=>\(E=MN\cap\left(SAC\right)\)

2:
a: \(B\in SB\)
\(B\in\left(ABC\right)\)
Do đó: \(B=SB\cap\left(ABC\right)\)
b: Chọn mp(SAB) có chứa BH
\(SA\subset\left(SAB\right)\)
\(SA\subset\left(SAC\right)\)
Do đó: \(\left(SAB\right)\cap\left(SAC\right)=SA\)
Gọi E là giao của BH và SA
=>E là giao điểm cần tìm
c: Chọn mp(SBC) có chứa BK
\(SC\subset\left(SBC\right)\)
\(SC\subset\left(SAC\right)\)
Do đó: \(\left(SBC\right)\cap\left(SAC\right)=SC\)
Gọi F là giao của BK với SC
=>F là giao điểm cần tìm
d: Trong mp(SAC), gọi O là giao của HK với AC
mà \(AC\subset\left(ABC\right)\)
nên \(O=HK\cap\left(ABC\right)\)