Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giải:
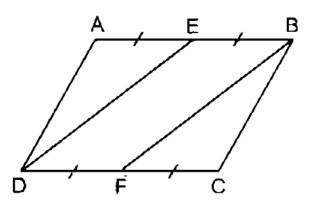
Ta có: AB = CD ( tính chất hình bình hành)
\(EB=\frac{1}{2}AB\left(gt\right)\)
\(FD=\frac{1}{2}CD\left(gt\right)\)
Suy ra: EB = FB (1)
Mà AB // CD (gt)
⇒ BE // FD (2)
Từ (1) và (2) suy ra tứ giác BEDF là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau)
⇒ DE = BF (tính chất hình bình hành)
Ta có: AB = CD (tính chất hình bình hành)
EB = 1/2 AB (gt)
FD = 1/2 CD (gt)
Suy ra: EB = FD (1)
Mà AB // CD (gt)
⇒ BE // FD (2)
Từ (1) và (2) suy ra tứ giác BEDF là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau)
⇒ DE = BF (tính chất hình bình hành)

Ta có \(EB=\dfrac{1}{2}AB\left(E.là.trung.điểm.AB\right)\)
\(FD=\dfrac{1}{2}CD\left(F.là.trung.điểm.CD\right)\)
\(AB=CD\left(hbh.ABCD\right)\Rightarrow\dfrac{1}{2}AB=\dfrac{1}{2}CD\)
\(\Rightarrow BE=DF;BE//DF\left(AB//CD\right)\)
Do đó BEDF là hbg
\(\Rightarrow DE=BF\)

a: BE=AB/2
DF=DC/2
mà AB=DC
nên BE=DF
Xét tứ giác BEDF có
BE//DF
BE=DF
=>BEDF là hình bình hành
=>DE=BF
b: BEDF là hbh
=>BD cắt EF tại trung điểm của mỗi đường(1)
ABCD là hbh
=>AC cắt BD tại trung điểm của mỗi đường(2)
Từ (1), (2) suy ra AC,BD,EF đồng quy

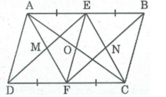
+) Ta có:
AE = 1/2 AB; CF = 1/2. CD ( vì E và F lần lượt là trung điểm của AB, CD).
Và AB = CD (tính chất hình bình hành)
Suy ra: AE = CF
+) Lại có: AB // CD ( vì ABCD là hình bình hành) nên AE //CF
Tứ giác AECF có hai cạnh đối AE, CF song song và bằng nhau nên là hình bình hành
⇒ AF //CE hay EN // FM (1)
Xét tứ giác BFDE ta có:
AB // CD (gt) hay BE // DF
BE = 1/2 AB (gt)
DF = 1/2 CD (gt)
AB = CD (tính chất hình bình hành)
Suy ra: BE = DF
Tứ giác BFDE là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau) ⇒ BF//DE hay EM // FN (2)
Từ (1) và (2) suy ra tứ giác EMFN là hình bình hành (theo định nghĩa hình bình hành)

Xét tứ giác AECF có
AE//CF
AE=CF
Do đó: AECF là hình bình hành

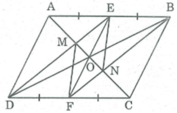
Xét ∆ EOM và ∆ FON có: ∠ (MEO) = ∠ (NFO) (so le trong do DE//BF)
OE = OF (tính chất hình bình hành)
∠ (MOE)= ∠ (NOF) (đối đỉnh )
Suy ra: ∆ EOM = ∆ FON (g.c.g) ⇒ OM = ON
Vậy tứ giác EMFN là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm mỗi đường).

5. Vì tứ giác ABCD là hình bình hành (gt)
=> AD // BC ; AD = BC (tc)
Vì M là trung điểm AD (gt)
N là trung điểm BC (gt)
AD = BC (cmt)
=> AM = DM = BN = CN
Vì AD // BC mà M ∈ AD, N ∈ BC
=> MD // BN
Xét tứ giác MBND có : MD = BN (cmt)
MD // BN (cmt)
=> Tứ giác MBND là hình bình hành (DHNB)
=> BM = DN (tc hình bình hành)
6. Vì tứ giác ABCD là hình bình hành (gt)
=> AB // CD ; AB = CD (tc)
Vì E là trung điểm AB (gt)
F là trung điểm CD (gt)
AB = CD (cmt)
=> AE = BE = DF = DF
Vì AB // CD mà E ∈ AB, F ∈ CD
=> BE // DF
Xét tứ giác DEBF có : BE = DF (cmt)
BE // DF (cmt)
=> Tứ giác DEBF là hình bình hành (DHNB)

Ta có: AB = CD (tính chất hình bình hành)
EB = 1/2 AB (gt)
FD = 1/2 CD (gt)
Suy ra: EB = FD (1)
Mà AB // CD (gt)
⇒ BE // FD (2)
Từ (1) và (2) suy ra tứ giác BEDF là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau)
⇒ DE = BF (tính chất hình bình hành)