Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Pt hoành độ giao điểm:
\(2x+m=\frac{x+3}{x+1}\Leftrightarrow2x^2+\left(m+1\right)x+m-3=0\)
\(\Delta=\left(m+1\right)^2-8\left(m-3\right)=\left(m-3\right)^2+16>0\)
\(\left\{{}\begin{matrix}x_1+x_2=-\frac{m+1}{2}\\x_1x_2=\frac{m-3}{2}\end{matrix}\right.\)
Ta có: \(MN^2=\left(x_1-x_2\right)^2+\left(y_1-y_2\right)^2\)
\(=5\left(x_1-x_2\right)^2=5\left(x_1+x_2\right)^2-20x_1x_2\)
\(=5\left(-\frac{m+1}{2}\right)^2-20\left(\frac{m-3}{2}\right)=\frac{5}{4}\left(m-3\right)^2+20\ge20\)
Dấu "=" xảy ra khi \(m=3\)

Đáp án DPhương trình hoành độ gaio điểm của đồ thị (C) và đường thẳng 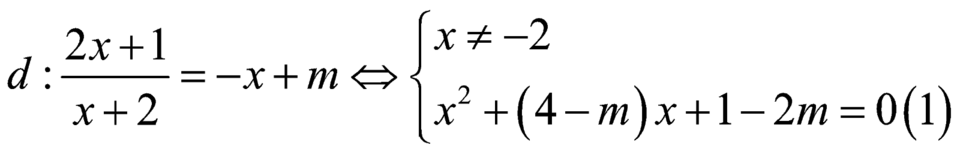
Gọi ![]() . Ta tính được
. Ta tính được ![]() khi m = 0
khi m = 0

Đề bài ko đúng
\(y=\frac{x-1}{x+1}\Rightarrow y'=\frac{2}{\left(x+1\right)^2}>0\) hàm số đồng biến
\(y=2x+m\) cũng luôn đồng biến do đó \(y=2x+m\) có thể tiếp xúc (C)
\(\Rightarrow AB\rightarrow0\) nên ko thể tồn tại m thỏa mãn
Nếu \(y=-2x+m\) thì còn có thể tồn tại m

a) y=x+3x+1y=x+3x+1 có tập xác định : R\{-1}
y′=−2(x+1)2<0,∀x≠−1y′=−2(x+1)2<0,∀x≠−1
Tiệm cận đứng: x = -1
Tiệm cận ngang: y = 1
Bảng biến thiên:
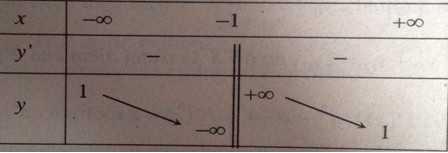
Đồ thị hàm số:
b) Xét phương trình có nghiệm là hoành độ giao điểm của (C) và đường thẳng (d): y = 2x + m
(1)
x+3x+1=2x+m⇔x+3=(2x+m)(x+1)⇔2x2+(m+1)x+m−3=0,x≠−1x+3x+1=2x+m⇔x+3=(2x+m)(x+1)⇔2x2+(m+1)x+m−3=0,x≠−1
Δ = (m+1)2 – 4.2(m-3) = m2 – 6m + 25 = (m-3)2 + 16> 0, Δm, nên (1) luôn có hai nghiệm phân biệt khác -1.
Vậy (d) luôn cắt (C) tại hai điểm phân biệt M, N (hoành độ của M, N chính là nghiệm của (1)).

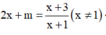



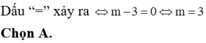

Lời giải:
Phương trình hoành độ giao điểm:
\(2x+m-\left(x+\frac{3}{x}+1\right)=0\)
\(\Leftrightarrow x^2+x(m-1)-3=0\)
Để hai đths cắt nhau tại hai điểm phân biệt thì pt trên phải có hai nghiệm phân biệt.
\(\Rightarrow \Delta=(m-1)^2+3>0\) (luôn đúng với mọi m)
Khi đó, gọi \(x_1,x_2\) là hai nghiệm của pt thì theo hệ thức Viete:
\(\left\{\begin{matrix} x_1+x_2=1-m\\ x_1x_2=-3\end{matrix}\right.\)
Hai giao điểm là \(M(x_1,2x_1+m); N(x_2,2x_2+m)\)
\(MN=\sqrt{(x_1-x_2)^2+(2x_1+m-2x_2-m)^2}=\sqrt{5(x_1-x_2)^2}\)
Có \((x_1-x_2)^2=(x_1+x_2)^2-4x_1x_2=(m-1)^2+12\geq 12\)
\(\Rightarrow MN\geq \sqrt{60}\) hay \(MN_{\min}=\sqrt{60}\)
Dấu bằng xảy ra khi \(m=1\)