

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

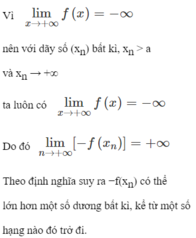


Vì 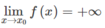
nên với dãy số ( x n ) bất kì, x n ∈ K \ x 0 và x n → x 0 ta luôn có
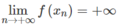
Từ định nghĩa suy ra f ( x n ) có thể lớn hơn một số dương bất kì, kể từ một số hạng nào đó trở đi.
Nếu số dương này là 1 thì f ( x n ) > 1 kể từ một số hạng nàođó trởđi.
Nói cách khác, luôn tồn tạiít nhất một số x k ∈ K \ x 0 sao cho f ( x k ) > 1 .

Đặt 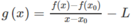
Suy ra g(x) xác định trên
(
a
;
b
)
\
x
0
và 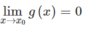
Mặt khác, f ( x ) = f ( x 0 ) + L ( x − x 0 ) + ( x − x 0 ) g ( x ) nên
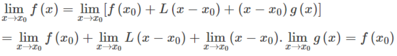
Vậy hàm số y = f(x) liên tục tại

Giả sử ( x n ) là dãy số bất kì thoả mãn n < a và x n → − ∞
Vì 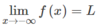 nên
nên 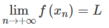
Vì 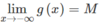 nên
nên 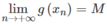
Do đó, 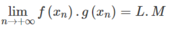
Từ định nghĩa suy ra 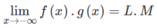

Thịnh ơi, có gì mấy câu trả lời SGK em giúp anh trình bày đầy đủ và làm đẹp nhé, có Latex đầy đủ á. Mình làm hướng đến cộng đồng, em giúp hoc24 nhé!
a) Ta có: \(\Delta x = x - {x_0},\Delta y = f\left( {{x_0} + \Delta x} \right) - f\left( {{x_0}} \right)\)
\(\begin{array}{l}\mathop {\lim }\limits_{\Delta x \to 0} \frac{{h({x_0} + \Delta x) - h({x_0})}}{{\Delta x}} = \mathop {\lim }\limits_{\Delta x \to 0} \frac{{h\left( x \right) - h\left( {{x_0}} \right)}}{{x - {x_0}}} = \mathop {\lim }\limits_{\Delta x \to 0} \frac{{f(x) + g(x) - f({x_0}) - g\left( {{x_0}} \right)}}{{x - {x_0}}}\\ = \mathop {\lim }\limits_{\Delta x \to 0} \frac{{g(x) - f\left( {{x_0}} \right)}}{{x - {x_0}}} + \mathop {\lim }\limits_{\Delta x \to 0} \frac{{f(x) - g\left( {{x_0}} \right)}}{{x - {x_0}}}\\ = \mathop {\lim }\limits_{\Delta x \to 0} \frac{{g\left( {{x_0} + \Delta x} \right) - f\left( {{x_0}} \right)}}{{\Delta x}} + \mathop {\lim }\limits_{\Delta x \to 0} \frac{{f\left( {{x_0} + \Delta x} \right) - g\left( {{x_0}} \right)}}{{\Delta x}}\end{array}\)
b) \(h'({x_0})\) = \(f'({x_0}) + g'({x_0})\)