Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có:
Do ˆxOyxOy^ và ˆxOy′xOy′^ là 2 góc kề bù
⇒⇒ˆxOyxOy^ + ˆxOy′xOy′^ = 180o
⇒⇒60o + ˆxOy′xOy′^ = 180o
⇒⇒ˆxOy′xOy′^ = 180o - 60o = 120o
Vậy ˆxOy′xOy′^= 120o
Ta có:
Do ˆxOyxOy^và góc ˆx′Oy′x′Oy′^ là 2 góc đối đỉnh
⇒⇒ˆxOy=ˆx′Oy′=60oxOy^=x′Oy′^=60o
Ta có:
Do ˆxOyxOy^ và ˆx′Oyx′Oy^ là 2 góc kề bù
⇒ˆxOy+ˆx′Oy=180o⇒xOy^+x′Oy^=180o
⇒60o+ˆx′Oy=180o⇒60o+x′Oy^=180o
⇒ˆx′Oy=180o−60o=120o⇒x′Oy^=180o−60o=120o
Vậy ˆx′Oy=120ox′Oy=120o^
Hoặc bạn có thể giải bằng cách này thì ngắn gọn hơn
Ta có:
Do ˆxOy′xOy′^ và ˆx′Oyx′Oy^ là hai góc đối đỉnh
⇒ˆxOy′=ˆx′Oy=120o⇒xOy′^=x′Oy^=120o
Vậy ˆx′Oy=120o
Có: góc xOy+ góc xOy'=180o(kề bù)
suy ra: góc xOy'=180o - góc xOy=180o - 60o=120o
góc x'Oy'= góc xOy=60o( đối đỉnh)
Lại có: góc x'Oy=góc xOy'=120o(đối đỉnh)
CHÚC BẠN HỌC TỐT

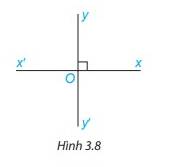
Góc x’Oy’ và xOy là hai góc đối đỉnh nên \(\widehat {x'Oy'} = \widehat {xOy} = 90^\circ \)
Góc xOy’ và xOy là hai góc kề bù nên
\(\begin{array}{l}\widehat {xOy'} + \widehat {xOy} = 180^\circ \\ \Rightarrow \widehat {xOy'} + 90^\circ = 180^\circ \\ \Rightarrow \widehat {xOy'} = 180^\circ - 90^\circ = 90^\circ \end{array}\)
Góc x’Oy và xOy là hai góc kề bù nên
\(\begin{array}{l}\widehat {x'Oy} + \widehat {xOy} = 180^\circ \\ \Rightarrow \widehat {x'Oy} + 90^\circ = 180^\circ \\ \Rightarrow \widehat {x'Oy} = 180^\circ - 90^\circ = 90^\circ \end{array}\)

\(a,\widehat{x'Oy'}=\widehat{xOy}=70^0\left(2.góc.đđ\right)\)
\(b,\widehat{x'Oy}.đối.đỉnh.\widehat{xOy'}\) do \(Ox.đối.Ox';Oy.đối.Oy'\)
\(c,\widehat{xOy'}+\widehat{xOy}=180^0\left(kề.bù\right)\\ \Rightarrow\widehat{xOy'}=180^0-70^0=110^0\\ \widehat{xOy'}=\widehat{x'Oy}=110^0\left(đối.đỉnh\right)\)

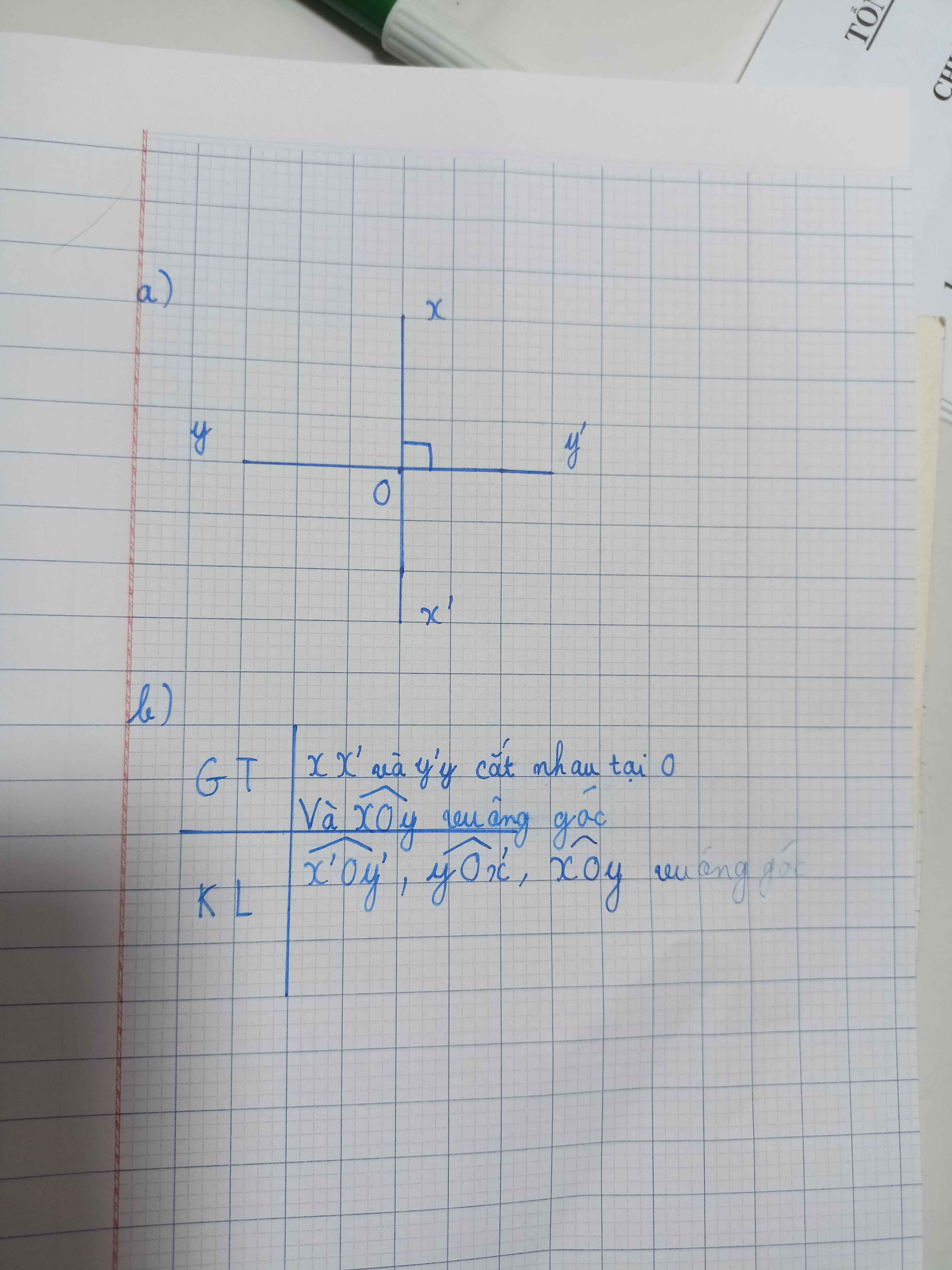
a) Các cặp góc đối đỉnh là:
\(\widehat{xOy}\) và \(\widehat{x'Oy'}\); \(\widehat{x'Oy}\) và \(\widehat{y'Ox}\).
b) + Có tia Ot là tia phân giác của góc xOy
\(\Rightarrow\widehat{xOt}=\widehat{yOt}=\dfrac{\widehat{xOy}}{2}\)
+ Có tia Oz là tia phân giác của góc x'Oy'
\(\Rightarrow\widehat{x'Oz}=\widehat{y'Oz}=\dfrac{\widehat{x'Oy'}}{2}\)
+ Có hai góc xOy' và góc xOy là hai góc kề bù
\(\Rightarrow\widehat{xOy}'+\widehat{xOy}=180^o\)
+ Có hai góc xOy và góc x'Oy' là một cặp góc đối đỉnh
\(\Rightarrow\) \(\widehat{xOy}=\widehat{x'Oy'}\)
\(\Rightarrow\dfrac{\widehat{xOy}}{2}=\dfrac{\widehat{x'Oy'}}{2}\)
\(\Rightarrow\widehat{xOt}=\widehat{y'Oz}=\dfrac{\widehat{xOy}}{2}\)
\(\Rightarrow\widehat{xOt}+\widehat{xOy'}+\widehat{y'Oz}=2\cdot\dfrac{\widehat{xOy}}{2}+\widehat{xOy'}=\widehat{xOy}+\widehat{xOy'}=\widehat{zOt}=180^o\)
nên hai tia Ot và Oz là hai tia đối nhau.
Mong cái này giúp được bạn nhé. ☺
a) Em dự đoán xem hai góc xOy và x’Oy’ có bằng nhau.
b) \(\widehat{xOy} = \widehat{x’Oy’} = 31^0\)