Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
+ Tọa độ giao điểm của hai đường thẳng d và d’ là nghiệm của hệ phương trình:
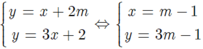
suy ra d và d’ cắt nhau tại M( m-1; 3m-1)
+ Vì ba đường thẳng d; d’ ; d’’ đồng quy nên d’’ qua M ta có
3m-1= -m( m-1) + 2 hay m2+ 2m-3=0
Suy ra m=1 hoặc m= -3
Với m= 1 ta có ba đường thẳng là d: y= x+ 2; d’ : y= 3x+ 2 và d’’: y= -x+ 2 phân biệt và đồng quy tại M(0; 2).
Với m= -3 ta có d và d’’ trùng nhau suy ra m= -3 không thỏa mãn
Vậy m= 1 là giá trị cần tìm.
Chọn B.

Phương trình hoành độ giao điểm:
`mx-3=x^2`
`<=>x^2-mx+3=0` (1)
(P) cắt (d) tại 2 điểm phân biệt `<=>` PT (1) có 2 nghiệm phân biệt.
`<=> \Delta >0`
`<=>m^2-3>0`
`<=> m<-\sqrt3 \vee m>\sqrt3`
Viet: `{(x_1+x_2=m),(x_1x_2=3):}`
`|x_1-x_2|=2`
`<=>(x_1-x_2)^2=4`
`<=> (x_1+x_2)^2-4x_1x_2=4`
`<=>m^2-4.3=4`
`<=>m= \pm 4` (TM)
Vậy....

Phương trình hoành độ giao điểm:
\(x^2+3x=x+m^2\Leftrightarrow x^2+2x-m^2=0\)
Pt đã cho luôn có 2 nghiệm pb
\(\left\{{}\begin{matrix}x_1+x_2=-2\\x_1x_2=-m^2\end{matrix}\right.\)
Do I là trung điểm đoạn AB \(\Leftrightarrow\left\{{}\begin{matrix}x_I=\dfrac{x_A+x_B}{2}=-1\\y_I=\dfrac{y_A+y_B}{2}=\dfrac{x_A+m^2+x_B+m^2}{2}=m^2-1\end{matrix}\right.\)
Mà I thuộc d'
\(\Leftrightarrow y_I=2x_I+3\Leftrightarrow m^2-1=2.\left(-1\right)+3\)
\(\Leftrightarrow m^2=2\Rightarrow m=\pm\sqrt{2}\)
\(\Rightarrow\sum m^2=4\)

Đáp án C