Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

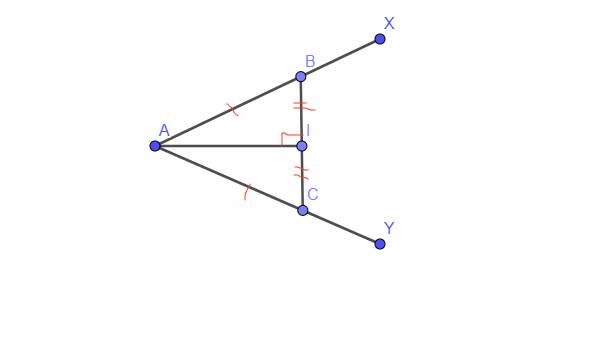
`a,` Xét Tam giác `AIB` và Tam giác `AIC` có:
`AB = AC (g``t)`
AI chung
`IB = IC (g``t)`
`=>` Tam giác `AIB =` Tam giác `AIC (c-c-c)`
`b,` Vì Tam giác `AIB =` Tam giác `AIC (a)`
`=>` \(\widehat{AIB}=\widehat{AIC}\) (2 góc tương ứng)
Mà 2 góc này ở vị trí kề bù
`=>` \(\widehat{AIB}+\widehat{AIC}=180^0\)
`=>` \(\widehat{AIB}=\widehat{AIC}=\) \(\dfrac{180}{2}=90^0\)
`=>` \(AI\perp BC\)
Tam giác `ABC` có `IB = IC`, \(AI\perp BC\)
`=> AI` là đường trung trực của `BC (đpcm)`

a: Xét ΔAIB và ΔAIC có
AI chung
IB=IC
AB=AC
Do đó: ΔAIB=ΔAIC

a) C/m tam giác AIB = tam giác AIC.
Xét tam giác AIB và tam giác AIC có :
AB = AC (GT)
AI chung
BI = IC ( do I trung điểm BC)
=> Tam giác AIB = tam giác AIC ( c_c_c).
-> Góc BIA = góc CIA ( tương ứng).
b) Có : góc BIA + góc CIA = 1800 (kề bù)
mà góc BIA = góc CIA -> góc BIA = góc CIA = 900.
=> AI vuông góc với BC (1)
mà BI = IC ( cmt ) (2)
(1) , (2) => AI là đường trung trực của BC.

a: Xét ΔOAB và ΔOAC có
OA chung
\(\widehat{BAO}=\widehat{CAO}\)
OB=OC
Do đó: ΔOAB=ΔOAC
b: Xét ΔOBM và ΔOCN có
OB=OC
\(\widehat{OBM}=\widehat{OCN}\)
BM=CN
Do đó: ΔOBM=ΔOCN