Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B.
Ta có: 1 + cos2α = 2cos2α và sin2α = 2sinα.cosα.
Mà tanα = 2 nên cot α = 1/2
Suy ra:
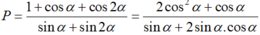
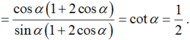

Hai góc α và β phụ nhau nên sin α = cos β ; cos α = sin β .
Do đó, P = cos α cos β − sin β sin α = cos α sin α − cos α sin α = 0 .
Chọn A.

Hai góc α và β phụ nhau nên sin α = cos β ; cos α = sin β .
Do đó, P = sin α cos β + sin β cos α = sin 2 α + cos 2 α = 1 .
Chọn B.

Đáp án B
c o s 2 α = 1 − s i n 2 α = 1 − 12 13 2 = 25 169 .
D o 90 ° < α < 180 ° nên cos α < 0 ⇒ cos α = − 5 13

Chọn D.
Xét biểu thức (sin α - cosα ) 2 + (sin α + cosα ) 2 ta có:
(sin α - cosα ) 2 + (sin α + cosα ) 2
= sin 2 α - 2sin α.cosα + cos 2 α + sin 2 α + 2 sin α.cosα + cos 2 α
= 2( sin 2 α + cos 2 α ) =2
⇒ (sin α - cosα ) 2 = 2 - (sin α + cosα ) 2
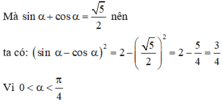
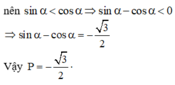

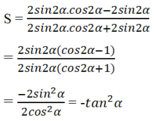
Đáp án: A
Ta cũng có thể suy luận cos2α – 1 < 0, cos2α + 1 > 0 nên S < 0, do đó các phương án B, C, D bị loại. Vậy đáp án là A.
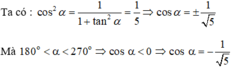
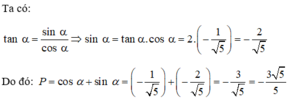
Đáp án A
P = s i n 2 90 ° − α + s i n 2 α = c o s 2 α + s i n 2 α = 1