K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 7 2021
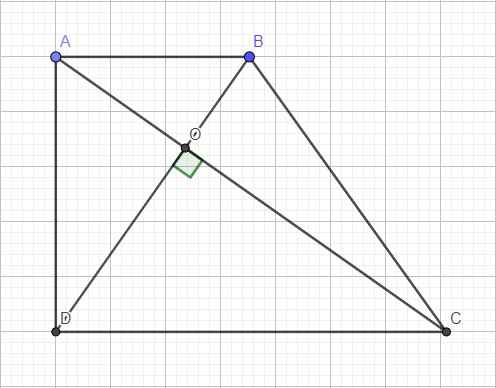
Xét tam giác vuông OAB:
\(OB=\sqrt{AB^2-OA^2}=4\)
Áp dụng hệ thức lượng cho tam giác vuông ABD với đường cao AO:
\(AB^2=OB.BD\Rightarrow BD=\dfrac{AB^2}{OB}=13\)
\(\Rightarrow\left\{{}\begin{matrix}OD=BD-OB=9\\AD=\sqrt{BD^2-AB^2}=\sqrt{29}\end{matrix}\right.\)
\(\widehat{BAO}=\widehat{DCO}\left(slt\right)\Rightarrow\Delta_VAOB\sim\Delta_VCOD\) (g.g)
\(\Rightarrow\dfrac{AB}{DC}=\dfrac{OB}{OD}\Rightarrow DC=\dfrac{AB.OD}{OB}=\dfrac{9\sqrt{13}}{2}\)
\(S_{ABCD}=\dfrac{1}{2}AD.\left(AB+CD\right)=\dfrac{1}{2}.\sqrt{29}.\left(2\sqrt{13}+\dfrac{9\sqrt{13}}{2}\right)=...\)
AB=2\(\sqrt{13}\)hay 2\(\sqrt{12}\)vậy?? căn 12 còn dễ tính chứ căn 13 lẻ toác cả bài.
sin... = \(\frac{6}{2\sqrt{12}}=\frac{\sqrt{3}}{2}\)=> góc =>tính ra cạnh
Hình tự vẽ nhé :v
Ta có: \(AC\perp BD\Rightarrow\widehat{AOB}=9\)
\(\widehat{AOB}=\widehat{O}=90^o\Rightarrow AO^2+OB^2=AB^2\)
\(\Rightarrow OB^2=AB^2-AO^2\)
\(=\left(2\sqrt{13}\right)^2-6^2\)
\(=16\) (cm)
\(\Delta ABD=\widehat{A}=90^o\) ; AO là đường cao
\(\Rightarrow AB^2=BO.BD\)
\(\Rightarrow BD=\frac{AB^2}{BO}\)
\(=\frac{\left(2\sqrt{13}\right)^2}{4}\)
\(=13\) (cm)
+) \(AB^2+AD^2=BD^2\)
\(\Rightarrow AD^2=BD^2-AB^2\)
\(=13^2-\left(2\sqrt{13}\right)^2\)
\(=3\sqrt{13}\) (cm)
\(\Delta ADC=\widehat{D}=90^o\) ; DO là đường cao
\(\Rightarrow AD^2=AO.AC\)
\(\Rightarrow AC=\frac{AD^2}{AO}=\frac{117}{6}=\frac{39}{2}\)
+) \(AD^2+DC^2=AC^2\)
\(\Rightarrow DC^2=\left(\frac{39}{2}\right)^2-\left(3\sqrt{13}\right)\)
\(\Rightarrow DC=\frac{9\sqrt{13}}{2}\)
\(\Rightarrow S_{ABCD}=\frac{1}{2}.AD.\left(AB+CD\right)\)
\(=\frac{1}{2}.3\sqrt{13}.\left(2\sqrt{3}+\frac{9\sqrt{13}}{2}\right)\)
\(=126,75\)