Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

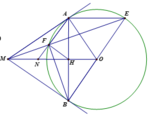
1) Chứng minh: Tứ giác MAOB nội tiếp một đường tròn
Vẽ được các yếu tố để chứng minh phần (1).
Ta có M B O ^ = 90 0 , M A O ^ = 90 0 (theo t/c của tiếp tuyến và bán kính)
Suy ra: M A O ^ + M B O ^ = 180 0 .Vậy tứ giác MAOB nội tiếp đường tròn.
2) Chứng minh: MN2 = NF. NA và MN = NH
Ta có A E / / M O ⇒ A E M ^ = E M N ^ mà A E M ^ = M A F ^ ⇒ E M N ^ = M A F ^
Δ N M F v à Δ N A M có: M N A ^ chung; E M N ^ = M A F ^
nên Δ N M F đồng dạng với Δ N A M
⇒ N M N F = N A N M ⇒ N M 2 = N F . N A 1
Mặt khác có: A B F ^ = A E F ^ ⇒ A B F ^ = E M N ^ h a y H B F ^ = F M H ^
=> MFHB là tứ giác nội tiếp
⇒ F H M ^ = F B M ^ = F A B ^ h a y F H N ^ = N A H ^
Xét Δ N H F & Δ N A H c ó A N H ^ c h u n g ; N H F ^ = N A H ^
=> Δ N M F đồng dạng Δ N A H ⇒ ⇒ N H N F = N A N H ⇒ N H 2 = N F . N A 2
Từ (1) và (2) ta có NH = HM
3) Chứng minh: H B 2 H F 2 − EF M F = 1 .
Xét Δ M AF và Δ M E A có: A M E ^ chung, M A F ^ = M E A ^
suy ra Δ M AF đồng dạng với Δ M E A
⇒ M E M A = M A M F = A E A F ⇒ M E M F = A E 2 A F 2 (3)
Vì MFHB là tứ giác nội tiếp ⇒ M F B ^ = M H B ^ = 90 0 ⇒ B F E ^ = 90 0 và A F H ^ = A H N ^ = 90 0 ⇒ A F E ^ = B F H ^
Δ A E F và Δ H B F có: E F A ^ = B F H ^ ; F E A ^ = F B A ^
suy ra Δ A E F ~ Δ H B F
⇒ A E A F = H B H F ⇒ A E 2 A F 2 = H B 2 H F 2 (4)
Từ (3) và (4) ta có M E M F = H B 2 H F 2 ⇔ M F + F E M F = H B 2 H F 2 ⇔ 1 + F E M F = H B 2 H F 2 ⇔ H B 2 H F 2 − F E M F = 1

a: Xét ΔAOM vuông tại A có tan AOM=AM/OA=căn 3
nên góc AOM=60 độ
=>sđ cung nhỏ AI=60 độ
=>sđ cung lớn AI=300 độ
b: Xét (O) có
MA,MC là tiếp tuyến
nên MA=MC và OM là phân giác của góc COA(1)
Xét (O) có
NC,NB là tiếp tuyến
nên NC=NB và ON là phân giác của góc COB(2)
Từ (1), (2) suy ra góc MON=1/2*180=90 độ
Xét ΔMON vuông tại O có OC là đường cao
nên MC*CN=OC^2
=>AM*BN=R^2
c: góc IAC=90 độ-góc OIA
góc MAI=90 độ-góc OAI
mà góc OIA=góc OAI
nên góc IAC=góc IAM
=>AI là phân giác của góc MAC
mà MI là phân giác của góc AMC
nên I là tâm đường tròn nội tiếp ΔMAC

a: góc MAO+góc MCO=180 độ
=>MAOC nội tiếp
b: góc AKB=1/2*180=90 độ
=>AK vuông góc MB
=>MK*MB=MA^2
MA,MC là tiếp tuyến
=>MA=MC
mà OA=OC
nên OM là trung trực của AC
=>OM vuông góc AC tại H
=>MH*MO=MA^2=MK*MB
=>MH/MB=MK/MO
=>ΔMHK đồng dạng với ΔMBO
=>góc MHK=góc MBO=góc ACK
c: AK^2/AM^2+MK/MB
=MK*KB/MK*MB+MK/MB
=KB/MB+MK/MB=1