Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

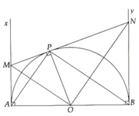
a, Sử dụng các tứ giác nội tiếp chứng minh được P M O ^ = P A O ^ và P N O ^ = P B O ^ => ∆MON và ∆APB đồng dạng (g.g)
b, Theo tính chất hai tiếp tuyến cắt nhau ta có: MP = MA và NP = NB
Mặt khác MP.NP = P O 2 và PO = R Þ AM.BN = R 2 (ĐPCM)
c, Ta có A M = R 2 => M P = R 2
Mặt khác A M = R 2 => BN = 2R => PN = 2R
Từ đó tìm được MN = 5 R 2
Vì DMON và DAPB đồng dạng nên S M O N S A P B = M N A B 2 = 25 16
d, Khi quay nửa đường tròn đường kính AB xung quanh AB ta được hình cầu với tâm O và bán kính R' = OA = R
Thể tích hình cầu đó là V = 4 3 πR 3 (đvdt)

Bài 1:
a,
OM là đường trung bình của tam giác BAC => OM = 1/2*BC
OM = 1/2*AB
=> AB=BC (đpcm).
b,
Tam giác ABC đều => BC = 2*r(O)
MN là đường trung bình của tam giác ABC => MN = 1/2*AB = r(O) = OM = OB =BN => BOMN là hình thoi.
a: Xét ΔAOM vuông tại A có tan AOM=AM/OA=căn 3
nên góc AOM=60 độ
=>sđ cung nhỏ AI=60 độ
=>sđ cung lớn AI=300 độ
b: Xét (O) có
MA,MC là tiếp tuyến
nên MA=MC và OM là phân giác của góc COA(1)
Xét (O) có
NC,NB là tiếp tuyến
nên NC=NB và ON là phân giác của góc COB(2)
Từ (1), (2) suy ra góc MON=1/2*180=90 độ
Xét ΔMON vuông tại O có OC là đường cao
nên MC*CN=OC^2
=>AM*BN=R^2
c: góc IAC=90 độ-góc OIA
góc MAI=90 độ-góc OAI
mà góc OIA=góc OAI
nên góc IAC=góc IAM
=>AI là phân giác của góc MAC
mà MI là phân giác của góc AMC
nên I là tâm đường tròn nội tiếp ΔMAC