Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

CẬu tự vẽ hình nha tớ vẽ hình gửi vào đây nó không cs hiện lên
a) Ta có góc OAM= góc OBM=90 độ (tính chất tiếp tuyến)
=> Tứ giác MAOB nội tiếp
b) xét tam giác MAC và tam giác MDA có
góc DMA chung
góc MAC= góc MDA=1/2 sđ cung AC
=> tam giác MAC đồng dạng tam giác MDA
=>\(\dfrac{AC}{AD}=\dfrac{MA}{MD}=\dfrac{MB}{MD}\)(vì MB=MA do tính chất 2 tiếp tuyến cắt nhau)(1)
xét tam giác MBC và tam giác MDB có
góc DMB chung
góc MBC = góc MDB=1/2 sđ cung BC
=> tam giác MBC đồng dạng MDB
=>\(\dfrac{BC}{DB}=\dfrac{MB}{MD}\)(2)
Từ (1) và (2)=>\(\dfrac{AC}{AD}=\dfrac{BC}{DB}\Rightarrow AC.BD=BC.AD\)

a: ΔOCD cân tại O có OK là đường trung tuyến
nên OK vuông góc CD
góc OKM=góc OAM=góc OBM=90 độ
=>O,K,M,A,B cùng thuộc đường tròn đường kính OM
b: Xét ΔMAC và ΔMDA có
góc MAC=góc MDA=1/2sđ cung AC
góc AMC chung
=>ΔMAC đồng dạng với ΔMDA
=>MA/MD=MC/MA
=>MA^2=MD*MC
=>MD*MC ko phụ thuộc vào cát tuyến MCD

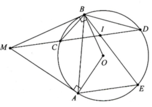
a, Vì M B C ^ = M D B ^ = 1 2 s đ C B ⏜ nên chứng minh được ∆MBC:∆MDB (g.g)
b, Vì
M
B
O
^
+
M
A
O
^
=
180
0
nên tứ giác MAOB nội tiếp
c, Đường tròn đường kính OM là đường tròn ngoại tiếp tứ giác MAOB => r = M O 2
Gọi H là giao điểm của AB với OM
=> OH ⊥ AB; AH = BH = R 3 2
Giải tam giác vuông OAM, đường cao AH ta được OM = 2R Þ r = R
d, Ta có M I B ^ = s đ D E ⏜ + s đ B C ⏜ 2 và M A B ^ = s đ A C ⏜ + s đ B C ⏜ 2
Vì AE song song CD => s đ D E ⏜ = s đ A C ⏜ => M I B ^ = M A B ^
Do tứ giác MAIB nội tiếp hay 5 điểm A, B, O, I, M nằm trên cùng 1 đường tròn kính MO
Từ đó ta có được M I O ^ = 90 0 => OI ⊥ CD hay I là trung điểm của CD