Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có: \(\angle ABO+\angle ACO=90+90=180\Rightarrow ABOC\) nội tiếp
Lại có: \(\angle AIO=\angle ABO=90\Rightarrow ABIO\) nội tiếp
\(\Rightarrow A,B,I,O,C\) cùng thuộc 1 đường tròn
\(\Rightarrow ABIC\) nội tiếp
\(\Rightarrow\angle AIB=\angle ACB=\angle ABC\) (\(\Delta ABC\) cân tại A) \(=\angle AIC\)
\(\Rightarrow IA\) là phân giác \(\angle CIB\)
b) Xét \(\Delta ABM\) và \(\Delta ANB:\) Ta có: \(\left\{{}\begin{matrix}\angle ABM=\angle ANB\\\angle NABchung\end{matrix}\right.\)
\(\Rightarrow\Delta ABM\sim\Delta ANB\left(g-g\right)\Rightarrow\dfrac{AB}{AN}=\dfrac{AM}{AB}\Rightarrow AB^2=AM.AN\)
mà \(AB^2=AH.AO\) (hệ thức lượng) \(\Rightarrow AH.AO=AM.AN\)
\(\Rightarrow\dfrac{AH}{AM}=\dfrac{AN}{AO}\)
Xét \(\Delta AHM\) và \(\Delta ANO:\) Ta có: \(\left\{{}\begin{matrix}\dfrac{AH}{AM}=\dfrac{AN}{AO}\\\angle NAOchung\end{matrix}\right.\)
\(\Rightarrow\Delta AHM\sim\Delta ANO\left(c-g-c\right)\Rightarrow\angle AHM=\angle ANO\)
\(\Rightarrow MHON\) nội tiếp \(\Rightarrow H\in\left(OMN\right)\)

a, Vì AM; AN lần lượt là tiếp tuyến đường tròn (O) với M;N là tiếp điểm
=> ^AMO = ^ANO = 900
mà AM = AN (tc tiếp tuyến cắt nhau) ; OM = ON = R
Vậy OA là đường trung trực đoạn MN => OA vuông MN
Xét tứ giác AMON có
^AMO + ^ANO = 1800
mà 2 góc này đối Vậy tứ giác AMON là tứ giác nt 1 đường tròn
b, Xét tam giác AMB và tam giác ACM có
^A _ chung ; ^AMB = ^ACB ( cùng chắn cung BM )
Vậy tam giác AMB ~ tam giác ACM (g.g)
\(\dfrac{AM}{AC}=\dfrac{AB}{AM}\Rightarrow AM^2=AB.AC\)
c, Xét tam giác OMA vuông tại M, đường cao MH
Ta có \(AM^2=AH.AO\)( hệ thức lượng )
=> \(AB.AC=AH.AO\Rightarrow\dfrac{AB}{AO}=\dfrac{AH}{AC}\)
Xét tam giác ABH và tam giác AOC có
^A _ chung
\(\dfrac{AB}{AO}=\dfrac{AH}{AC}\left(cmt\right)\)
Vậy tam giác ABH ~ tam giác AOC (c.g.c)
=> ^ABH = ^AOC ( góc ngoài đỉnh B )
Vậy tứ giác BHOC là tứ giác nt 1 đường tròn
d, Ta có BHOC nt 1 đường tròn (cmc)
=> ^OHC = ^OBC (góc nt chắc cung CO)
=> ^AHB = ^ACO (góc ngoài đỉnh H)
mà ^OCB = ^OBC do OB = OC = R nên tam giác OBC cân tại O
=> ^OHC = ^AHB
mà ^CHN = 900 - ^OHC
^NHB = 900 - ^AHB
=> ^CHN = ^NHB
=> HN là phân giác của ^BHC

a, Ta có AM ; AN lần lượt là tiếp tuyến (O)
=> ^AMO = ^ANO = 900
Xét tứ giác AMON có ^AMO + ^ANO = 1800
mà 2 góc này đối
Vậy tứ giác AMON là tứ giác nt 1 đường tròn
b, Xét tam giác AMB và tam giác ACM ta có
^A _ chung ; ^AMB = ^ACM ( cùng chắn BM )
Vậy tam giác AMB ~ tam giác ACM (g.g)
c, Ta có AM = AN ( tc tiếp tuyến cắt nhau )
ON = OM = R => OA là đường trung trực đoạn MN
Xét tam giác AMO vuông tại M, đường cao MH
=> AM^2 = AH.AO
=> AB . AC = AH . AO => AB/AO = AH/AC
Xét tam giác ABH và tam giác AOC có
^A _ chung ; AB/AO = AH/AC (cmt)
Vậy tam giác ABH ~ tam giác AOC (c.g.c)
=> ^ABH = ^AOC ( mà ^ABH là góc ngoài đỉnh B )
Vậy tứ giác BHOC là tứ giác nt 1 đường tròn

do I là trung điểm của MN
⇒I là trung trực của MN
⇒I⊥MN
⇒∠OIM=90⇔∠OIA=90
xét tứ giác ABIO có ∠OBA=∠OIA=90
⇒ABIO nội tiếp
⇒∠BIA=∠AOB (cùng chắn \(\stackrel\frown{AB}\)) (1)
xét tứ giác ACOI có ∠OIA=∠OCA=90
⇒ACOI nội tiếp
⇒∠AIC=∠AOC (cùng chắn \(\stackrel\frown{AC}\)) (2)
xét tứ giác ABOC nội tiếp đường tròn ; AB=AC
⇒∠AOB=∠AOC (chắn 2 cung = nhau) (3)
từ (1);(2);(3) ⇒∠BIA=∠AIC
⇒IA là tia phân giác ∠BIC

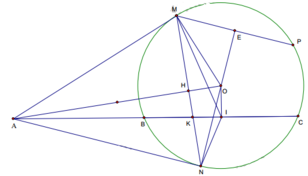
Theo giả thiết AMO = ANO = AIO = 90o = > 5 điểm A, O, M, N, I thuộc đường tròn đường kính AO 0,25
=> AIN = AMN, AIM = ANM (Góc nội tiếp cùng chắn một cung)
AM = AN => ∆AMN cân tại A => AMN = ANM
=> AIN = AIM => đpcm

Xét tg vuông AMO và tg vuông ANO có
AO chung; OM=ON (bán kính (O))
=> tg AMO = tg ANO (Hai tg vuông có 2 cạnh góc vuông bằng nhau)
\(\Rightarrow AM=AN\) (đpcm)
\(\Rightarrow\widehat{MAO}=\widehat{NAO}\) => AO là phân giác \(\widehat{MAN}\) (đpcm)
\(\Rightarrow\widehat{AOM}=\widehat{AON}\) => AO là phân giác \(\widehat{MON}\) (đpcm)

a: Xét (O) có
AB là tiếp tuyến
AC là tiếp tuyến
Do đó: AB=AC
hay A nằm trên đường trung trực của BC(1)
Ta có: OB=OC
nên O nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra AO là đường trung trực của BC
c)
Gọi giao điểm của MN với AC là G
Ta có: GEGM=GBGAGEGM=GBGA
Ta lại có GB . GC = GM . GN = GH . GA
⇒GBGA=GHGC⇒GBGA=GHGC
⇒GEGM=GHGC(đpcm)
Bạn nào thấymik làm đúng ko ạ