Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

(d) có vector chỉ phương là (1, -1) và vector pháp tuyến là (-1,1).
Đường thẳng đi qua M(2,1) và vuông góc với (d) có dạng:
\(\frac{x-2}{-1}=\frac{y-1}{1}\), hay là: x + y = 3
Hình chiếu của M trên (d) chính là giao điểm của 2 đường thẳng:
x + y = 3
x - y = 0
Giải hệ ra ta có x = y = 3/2
Vậy Hình chiếu là (3/2 ; 3/2)
Viết pt đường thẳng (a) qua M và vuông góc với (d)
(a) cắt (d) tại đâu ta được hình chiếu H của M

câu a
đường thẳng (d') là đường thẳng cần tìm
d' // d nên d' có dạng x-y +c = 0 với c khác 0
lấy điểm bất kì thuộc (d) là O(0,0) lấy đối xứng O qua M ta được O' ( 4, 2) vậy O' thuộc (d')
4−2+c=0⇒c=−2⇒(d′):x−y−2=0
Câu b
Viết pt đường thẳng (a) qua M và vuông góc với (d)
(a) cắt (d) tại đâu ta được hình chiếu H của M![]()

Lấy N (1;1) và P(0;0) thuộc (d)
Gọi N' ,P' là điểm đối xứng của N,P qua M
Ta có xN' = 2*2 -1= 3
yN'= 2*1-1 =1
xP'= 2*2-0=4
yP'= 2*1-0=2
==> N'(3;1), P'(4; 2)
(d') là đường thẳng đối xứng với M qua (d) ==> (d') đi qua N' , P'
==> Phương trình (d') \(\frac{x-3}{4-3}\)= \(\frac{y-1}{2-1}\)
==> x-y-2=0
Vậy (d') là x-y-2=0
Lấy N (1;1) và P(0;0) thuộc (d)
Gọi N' ,P' là điểm đối xứng của N,P qua M
Ta có xN' = 2*2 -1= 3
yN'= 2*1-1 =1
xP'= 2*2-0=4
yP'= 2*1-0=2
==> N'(3;1), P'(4; 2)
(d') là đường thẳng đối xứng với M qua (d) ==> (d') đi qua N' , P'
==> Phương trình (d') x−34−3= y−12−1
==> x-y-2=0
Vậy (d') là x-y-2=0

1. Gọi d' là đường thẳng qua A và vuông góc d
\(\Rightarrow\) d' nhận (1;3) là 1 vtpt
Phương trình d':
\(1\left(x+2\right)+3\left(y-3\right)=0\Leftrightarrow x+3y-4=0\)
H là giao điểm d và d' nên tọa độ thỏa mãn:
\(\left\{{}\begin{matrix}3x-y+4=0\\x+3y-4=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=-\dfrac{4}{5}\\y=\dfrac{8}{5}\end{matrix}\right.\)
\(\Rightarrow H\left(-\dfrac{4}{5};\dfrac{8}{5}\right)\)
2.
Do A' đối xứng A qua d nên H là trung điểm AA'
\(\Rightarrow\left\{{}\begin{matrix}x_{A'}=2x_H-x_A=\dfrac{2}{5}\\y_{A'}=2y_H-y_A=\dfrac{1}{5}\end{matrix}\right.\)
\(\Rightarrow A'\left(\dfrac{2}{5};\dfrac{1}{5}\right)\)
3.
Gọi B là giao điểm d và \(\Delta\) thì tọa độ B thỏa mãn:
\(\left\{{}\begin{matrix}3x-y+4=0\\x+2y-5=0\end{matrix}\right.\) \(\Rightarrow B\left(-\dfrac{3}{7};\dfrac{19}{7}\right)\)
Lấy điểm \(C\left(0;4\right)\) thuộc d
Phương trình đường thẳng \(d_1\) qua C và vuông góc \(\Delta\) có dạng:
\(2\left(x-0\right)-\left(y-4\right)=0\Leftrightarrow2x-y+4=0\)
Gọi D là giao điểm \(\Delta\) và \(d_1\Rightarrow\left\{{}\begin{matrix}x+2y-5=0\\2x-y+4=0\end{matrix}\right.\) \(\Rightarrow D\left(-\dfrac{3}{5};\dfrac{14}{5}\right)\)
Gọi D' là điểm đối xứng C qua \(\Delta\Rightarrow\) D là trung điểm CD'
\(\Rightarrow\left\{{}\begin{matrix}x_{D'}=2x_D-x_C=-\dfrac{6}{5}\\y_{D'}=2y_D-y_C=\dfrac{8}{5}\end{matrix}\right.\) \(\Rightarrow\overrightarrow{BD'}=\left(-\dfrac{27}{35};-\dfrac{39}{35}\right)=-\dfrac{3}{35}\left(9;13\right)\)
Phương trình đường thẳng đối xứng d qua denta (nhận \(\left(9;13\right)\) là 1 vtcp và đi qua D':
\(\left\{{}\begin{matrix}x=-\dfrac{6}{5}+9t\\y=\dfrac{8}{5}+13t\end{matrix}\right.\)

a.
Do d vuông góc với \(\Delta\) nên d nhận \(\left(1;-3\right)\) là 1 vtpt
Phương trình d:
\(1\left(x+1\right)-3\left(y-1\right)=0\Leftrightarrow x-3y+4=0\)
b.
\(M\in d\) mà \(MH\perp\Delta\Rightarrow\) H là giao điểm của d và \(\Delta\)
Tọa độ H là nghiệm của hệ:
\(\left\{{}\begin{matrix}x-3y+4=0\\3x+y-8=0\end{matrix}\right.\) \(\Rightarrow H\left(2;2\right)\)
c.
M' đối xứng với M qua \(\Delta\) khi và chỉ khi H là trung điểm MM'
Theo công thức trung điểm:
\(\left\{{}\begin{matrix}x_{M'}=2x_H-x_M=5\\y_{M'}=2y_H-y_M=3\end{matrix}\right.\) \(\Rightarrow M'\left(5;3\right)\)
Tại sao lại đổi từ (3; 1) sang (1; -3 ) vậy ạ? Denlta có dạng pttq thì có vtpt và đường thẳng d cũng vuông góc với denlta rồi mà?

Đường tròn \((C)\) tâm \(I(a;b)\) bán kính \(R\)có phương trình
\((x-a)^2+(y-b)^2=R^2.\)
\(∆MAB ⊥ M\) \(\rightarrow \) \(AB\) là đường kính suy ra \(∆\) qua \(I\) do đó:
\(a-b+1=0 (1)\)
Hạ \(MH⊥AB\) có \(MH=d(M, ∆)= \dfrac{|2-1+1|}{\sqrt{2}}={\sqrt{2}} \)
\(S_{ΔMAB}=\dfrac{1}{2}MH×AB \Leftrightarrow 2=\dfrac{1}{2}2R\sqrt{2} \)
\(\Rightarrow R = \sqrt{2} \)
Vì đường tròn qua\(M\) nên (\(2-a)^2+(1-b)^2=2 (2)\)
Ta có hệ :
\(\begin{cases} a-b+1=0\\ (2-a)^2+(1-b)^2=0 \end{cases} \)
Giải hệ \(PT\) ta được: \(a=1;b=2\).
\(\rightarrow \)Vậy \((C) \)có phương trình:\((x-1)^2+(y-2)^2=2\)
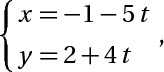 d2:
d2: 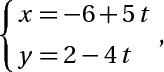
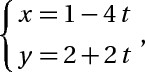 d2 : 2x+4y-10=0
d2 : 2x+4y-10=0
hinh dau
x - y = 0
x = y