Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vẽ S, đối xứng với S qua G .
\(\Rightarrow\)S,là ảnh của S qua G
Khoảng cách giữa S và S, ban đầu là :
SS,=50+50=100(cm)
Giả sử bây giờ S di chuyển tới S1
\(\Rightarrow\)SS1=15cm
Khi đó khoảng cách giữa S1 và S,là :
S1S,=SS,-SS1=100-15=85(cm)

Đáp án B
Vân sáng trung tâm sẽ dài theo phương song song với S 1 S 2 về phía S 1 một khoảng:
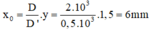

Cách giải: Đáp án C.
+ Gọi Δx là độ dịch chuyển của vân sáng, Δy là độ dịch chuyển của nguồn sáng .
Vân tối sáng bậc 2 thành vân tối bậc 2 => Δx = 5i
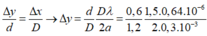
= 0,64 mm

Đáp án C.
+ Gọi ∆ x là độ dịch chuyển của vân sáng, ∆ y là độ dịch chuyển của nguồn sáng .
Vân tối sáng bậc 2 thành vân tối bậc 2 ![]()
+ Ta có
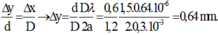

- Gọi Δx là độ dịch chuyển của vân sáng, Δ y là độ dịch chuyển của nguồn sáng.
→ Vân tối sáng bậc 2 thành vân tối bậc 2 → Δ x = 0,5i.
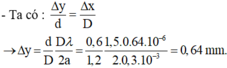
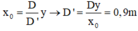
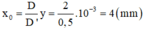

- Vẽ S, đối xứng với S qua G
\(\Rightarrow\)S, là ảnh của S qua G
\(\Rightarrow\)SS,=30.2=60cm
-Gọi S1 là vị trí của S sau khi di chuyển // với G 1 đoạn 10cm
\(\Rightarrow SS_1=10cm\)
Xét tam giác vuông SS1S, có :
S1S,2=SS,2-SS12 (theo ĐL Py-ta -go)
\(\Rightarrow\)S1S,=\(\sqrt{SS^,^2-SS_1^2}=\sqrt{60^2-10^2}=10\sqrt{35}\)(cm)