Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

- Vẽ S, đối xứng với S qua G
\(\Rightarrow\)S, là ảnh của S qua G
\(\Rightarrow\)SS,=30.2=60cm
-Gọi S1 là vị trí của S sau khi di chuyển // với G 1 đoạn 10cm
\(\Rightarrow SS_1=10cm\)
Xét tam giác vuông SS1S, có :
S1S,2=SS,2-SS12 (theo ĐL Py-ta -go)
\(\Rightarrow\)S1S,=\(\sqrt{SS^,^2-SS_1^2}=\sqrt{60^2-10^2}=10\sqrt{35}\)(cm)

Chọn đáp án B
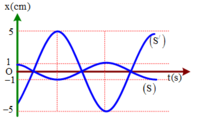
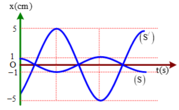
+ Từ đồ thị ta thấy, ảnh cao gấp 5 lần vật và ngược chiều vật (S và S’ dao động nghịch pha)
+ d / = 5 d 1 f = 1 d + 1 d / ⇔ 1 f = 1 d + 1 5 d ⇒ d = 6 c m ⇒ d / = 30 c m
+ Khoảng cách giữa hai vị trí của S và S’ là: L = d + d / = 36 c m
+ Khoảng cách lớn nhất giữa S và S’ theo phương dao động:
Δ x max = A S + A S / = 1 + 5 = 6 c m
+ Vậy S S / max = L 2 + Δ x max 2 = 36 2 + 6 2 = 36 , 497 c m

Chọn đáp án B
? Lời giải:
+ Từ đồ thị ta thấy, ảnh cao gấp 5 lần vật và ngược chiều vật (S và S’ dao động nghịch pha)

+ Khoảng cách lớn nhất giữa S và S’ theo phương dao động:
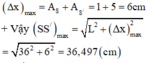

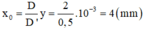
Vẽ S, đối xứng với S qua G .
\(\Rightarrow\)S,là ảnh của S qua G
Khoảng cách giữa S và S, ban đầu là :
SS,=50+50=100(cm)
Giả sử bây giờ S di chuyển tới S1
\(\Rightarrow\)SS1=15cm
Khi đó khoảng cách giữa S1 và S,là :
S1S,=SS,-SS1=100-15=85(cm)