Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét 2 tam giác vuôngΔBHM và ΔCKM có:
Góc M1 = M2 ( đối đỉnh)
BM = CM (gt)
⇒ ΔBHM = ΔCKM ( cạnh huyền góc nhọn)
⇒ BH = CK ( 2 cạnh tương ứng)
Vì góc H = M :
⇒ BH // CK ( so le trong)
a) Xét \(\Delta BMH,\Delta CMK\) có:
\(\widehat{BHM}=\widehat{CKM}\left(=90^{^O}\right)\)
\(BM=MC\) (M là trung điểm của BC)
\(\widehat{BMH}=\widehat{CMK}\)(đối đỉnh)
=> \(\Delta BMH=\Delta CMK\) (cạnh huyền - góc nhọn) (*)
=> \(\widehat{HBM}=\widehat{KCM}\) (2 góc tương ứng)
Mà thấy : 2 góc này ở vị trí so le trong
=> \(BH//CK\)
Từ (*) suy ra : \(BH=CK\)( 2 cạnh tương ứng)
b) Xét \(\Delta BKM,\Delta CHM\) có :
\(BM=MC\) (M là trung điểm của BC)
\(\widehat{BMK}=\widehat{CMH}\) (đối đỉnh)
\(HM=MK\) [suy ra từ (*)]
=> \(\Delta BKM=\Delta CHM\left(c.g.c\right)\) (**)
=> \(\widehat{KBM}=\widehat{HCM}\) (2 góc tương ứng)
Mà thấy : 2 góc này ở vị trí so le trong
=> \(BK//CH\left(đpcm\right)\)
Từ (**) suy ra : \(BK=CH\) (2 cạnh tương ứng)
c) Ta có : \(BK=CH\) (chứng minh trên -câub)
Lại có : \(\left\{{}\begin{matrix}CH=HF+FC\left(\text{F là trung điểm của CH}\right)\\BK=BE+EK\left(\text{E là trung điểm của BK}\right)\end{matrix}\right.\)
Suy ra : \(HF=FC=BE=EK\)
Xét \(\Delta HMF,\Delta KME\) có :
\(HF=EK\left(cmt\right)\)
\(\widehat{HMF}=\widehat{KME}\) (đối đỉnh)
\(HM=MK\) [từ (*)]
=> \(\Delta HMF=\Delta KME\left(c.g.c\right)\)
=> \(EM=FM\) (2 cạnh tương ứng)
=> M là trung điểm của EF
Do đó : E, M, F thẳng hàng
=> đpcm

a: Xét ΔABH vuông tại A và ΔMBH vuông tại M có
BH chung
\(\widehat{ABH}=\widehat{MBH}\)
Do đó:ΔABH=ΔMBH
b: ta có: ΔABH=ΔMBH
nên BA=BM; HA=HM
=>BH là đường trung trực của AM
c: Xét ΔANH vuông tại A và ΔMCH vuông tại M có
HA=HM
góc AHN=góc MHC
Do đó: ΔANH=ΔMCH
Suy ra: AN=MC
Xét ΔBNC có BA/AN=BM/MC
nên AM//NC

a) Xét tam giác HBM và tam giác KCM ,có :
MB = MC ( M là trung điểm của BC )
góc M1 = góc M2 ( đối đỉnh )
góc BHM = góc CKM ( = 90 độ )
=> tam giác HBM = tam giác KCM ( cạnh huyền - góc nhọn )
=> BH = CK ( hai cạnh tương ứng )
Vậy BH = CK
Vì góc góc BHM = góc CKM ( = 90 độ ) mà hai góc ở vị trí so le trong nên BH // CK ( dấu hiệu nhận biết hai đường thẳng song song )
Vậy BH // CK ; BH = CK ( đpcm )
b) Xét tam giác HMC và tam giác KMB , có :
góc M3 = góc M4 ( đối đỉnh )
MC = MB ( M là trung điểm của BC )
MH = MK ( tam giác HBM = tam giác KCM )
=> tam giác HMC = tam giác KMB ( c-g-c )
=> BK = CH ( hai cạnh tương ứng )
=> góc HCM = góc KBM ( hai góc tương ứng ) mà hai góc ở vị trí so le trong nên BK // CH ( dấu hiệu nhận biết hai đường thẳng song song )
Vậy BK = CH ; BK // CH ( đpcm )
c) Vì góc BMF + góc FMC = 180 độ ( hai góc kề bù ) mà góc FMC + góc CME = 180o ( hai góc kề bù ) => ba điểm E , M , F thẳng hàng
Vậy ba điểm E , M , F thẳng hàng
d) Bn tự làm nha!

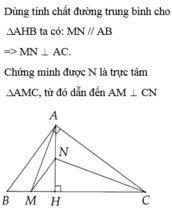
Goi giao NM voi AC la D
Xet tam giac BHA co N la trung diem BH , M la trung diem AH
=> NM la duong trung binh => NM // AB
ma AB vuong goc voi AC (gt)
Suy ra NM vuong goc voi AC ( tu vuong goc den song song)
Xet tam giac NAC co AH vuong goc voi NC (gt)
NM vuong goc voi AC ( cmt)
=> M la truc tam tam giac ANC
=> CM vuong goc voi AN
DPCM

Bài 1:
Sửa đề: Cho ΔABC vuông tại A
a: Xét ΔHAC có
M là trung điểm của HA
N là trung điểm của HC
Do đó: MN là đường trung bình
=>MN//AC
hay MN\(\perp\)AB
Xét ΔANB có
AH là đường cao
NM là đường cao
AH cắt NM tại M
DO đó:M là trực tâm của ΔANB
b: Tacó: M là trực tâm của ΔANB
nên BM\(\perp\)AN

d, cm tam giác EMK = tam giác FMH (c-g-c)
=> EM = MF => M là trđ của EF
Cm tam giác BEH = tam giác FHE (c-g-c) => BH // EF => EF _|_ AM
=> tam giác AEF cân tại A
không hiểu chỗ nào thì hỏi
a) Xét Δ B H M ; Δ C K M ΔBHM;ΔCKM có :
ˆ B H M = ˆ C K M ( = 90 o − g t )
BHM^=CKM^(=90o−gt)
B M = M C ( g t ) BM=MC(gt) ˆ H M B = ˆ K M C HMB^=KMC^ (đối đỉnh)
=> Δ B H M = Δ C K M ΔBHM=ΔCKM (cạnh huyền - góc nhọn)
=> ˆ H B M = ˆ K C M HBM^=KCM^ (2 góc tương ứng)
Mà 2 góc này ở vị trí so le trong
=> BH // KC ( đ p c m ) BH // KC(đpcm)
Và từ Δ B H M = Δ C K M ΔBHM=ΔCKM (cmt)
=> B H = C K BH=CK (2 cạnh tương ứng)
b) Xét Δ H M C ; Δ K M B ΔHMC;ΔKMB có :
B M = M C ( g t )
BM=MC(gt) ˆ H M C = ˆ K M B HMC^=KMB^ (đối đỉnh)
H M = M K HM=MK (do Δ B H M = Δ C K M ΔBHM=ΔCKM -cmt)
=> Δ H M C ; Δ K M B ΔHMC;ΔKMB
=> Δ H M C = Δ K M B ΔHMC=ΔKMB (c.g.c)
=> ˆ H C M = ˆ K B M HCM^=KBM^ (2 góc tương ứng)
Mà : 2 góc này ở vị trí so le trong
=> BK // CH ( đ p c m ) BK // CH (đpcm)
Có : Δ H M C = Δ K M B ΔHMC=ΔKMB (cmt)
=> B K = C H BK=CH (2 cạnh tương ứng)
c) Ta có : { H F = F C B E = E K {HF=FCBE=EK (gt)
Mà : B K = H C ( c m t ) BK=HC(cmt)
=> H F = F C = B E = E K HF=FC=BE=EK
Xét Δ B E M ; Δ F C M ΔBEM;ΔFCM có :
B M = M C ( g t ) BM=MC(gt) ˆ M B E = ˆ M C F ( s l t )
MBE^=MCF^(slt) B E = F C ( c m t ) BE=FC(cmt)
=> Δ B E M = Δ F C M ( c . g . c ) ΔBEM=ΔFCM(c.g.c)
=> E M = F M EM=FM(2 cạnh tương ứng)
=> M Là trung điểm của EF Do đó : E, ,M, F thẳng hàng
Bạn xem lại được không ạ? Chứ đề bài không sai đâu ạ
Mình vẫn vẽ được hình mà bạn