XC
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
17 tháng 9 2023
Bài 1: q=u2:u1=3:1=3
=> 3 số hạng tiếp theo: 81, 243, 729
Bài 2:
\(S_{11}=\dfrac{u_1.\left(q^{11}-1\right)}{q-1}=\dfrac{5.\left[\left(-2\right)^{11}-1\right]}{-2-1}\\ =\dfrac{5.\left(-2049\right)}{-3}=3415\)
10 tháng 9 2023
1: Để ba số này lập thành cấp số cộng thì
\(\left[{}\begin{matrix}x-1=2\left(2x+2x-4\right)\\2x=2\left(x-1+2x-4\right)\\2x-4=2\left(x-1+2x\right)\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}8x-8=x-1\\2x=6x-10\\2x-4=6x-2\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=1\\-4x=-10\\-4x=2\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=\dfrac{5}{2}\\x=-\dfrac{1}{2}\end{matrix}\right.\)
2: 11;15;19
CM
7 tháng 12 2017
a) Năm số hạng đầu là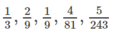 
b) Lập tỉ số
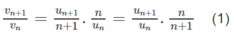
Theo công thứcđịnh nghĩa ta có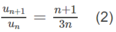 
Từ (1) và (2) suy ra
Vậy, dãy số ( v n ) là cấp số nhân, có v 1 = 1 / 3 , q = 1 / 3
c) Để tính ( u n ) , ta viết tích của n - 1 tỉ số bằng 1/3
NV
Nguyễn Việt Lâm
Giáo viên
16 tháng 12 2020
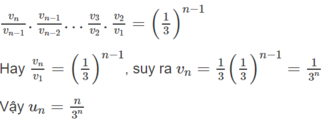
Câu 1:
Dãy đã cho có thể viết dưới dạng công thức truy hồi sau:
\(\left\{{}\begin{matrix}u_1=1\\u_{n+1}=u_n+7n\end{matrix}\right.\)
\(u_{n+1}=u_n+7n\Leftrightarrow u_{n+1}-\dfrac{7}{2}\left(n+1\right)^2+\dfrac{7}{2}\left(n+1\right)=u_n-\dfrac{7}{2}n^2+\dfrac{7}{2}n\)
Đặt \(v_n=u_n-\dfrac{7}{2}n^2+\dfrac{7}{2}n\Rightarrow\left\{{}\begin{matrix}v_1=1\\v_{n+1}=v_n\end{matrix}\right.\)
\(\Rightarrow v_{n+1}=v_n=v_{n-1}=...=v_1=1\)
\(\Rightarrow u_n-\dfrac{7}{2}n^2+\dfrac{7}{2}n=1\)
\(\Leftrightarrow u_n=\dfrac{7}{2}n^2-\dfrac{7}{2}n+1\)
\(\dfrac{7}{2}n^2-\dfrac{7}{2}n+1=35351\)
\(\Leftrightarrow\dfrac{7}{2}n^2-\dfrac{7}{2}n-35350=0\)
\(\Rightarrow n=101\)
Vậy đó là số hạng thứ 101
NV
Nguyễn Việt Lâm
Giáo viên
16 tháng 12 2020
2.
Do a;b;c lập thành 1 cấp số cộng
\(\Rightarrow a+c=2b\)
\(\Leftrightarrow2R.sinA+2R.sinC=2.2R.sinB\)
\(\Leftrightarrow sinA+sinC=2sinB\)
\(\Leftrightarrow2sin\dfrac{A+C}{2}.cos\dfrac{A-C}{2}=4sin\dfrac{B}{2}cos\dfrac{B}{2}\)
\(\Leftrightarrow cos\dfrac{B}{2}cos\dfrac{A-C}{2}=2sin\dfrac{B}{2}cos\dfrac{B}{2}\)
\(\Leftrightarrow cos\dfrac{A-C}{2}=2sin\dfrac{B}{2}=2cos\dfrac{A+C}{2}\)
\(\Leftrightarrow cos\left(\dfrac{A}{2}\right)cos\left(\dfrac{C}{2}\right)+sin\left(\dfrac{A}{2}\right)sin\left(\dfrac{C}{2}\right)=2cos\left(\dfrac{A}{2}\right)cos\left(\dfrac{C}{2}\right)-2sin\left(\dfrac{A}{2}\right)sin\left(\dfrac{C}{2}\right)\)
\(\Leftrightarrow cos\left(\dfrac{A}{2}\right).cos\left(\dfrac{C}{2}\right)=3sin\left(\dfrac{A}{2}\right).sin\left(\dfrac{C}{2}\right)\)
\(\Leftrightarrow cot\left(\dfrac{A}{2}\right).cot\left(\dfrac{C}{2}\right)=3\)
XC
1
HQ
Hà Quang Minh
Giáo viên
24 tháng 9 2023
\(u_n=u_1\cdot q^{n-1}\\ \Rightarrow\dfrac{3}{512}=\dfrac{3}{2}\cdot\left(\dfrac{1}{2}\right)^{n-1}\\ \Leftrightarrow\left(\dfrac{1}{2}\right)^{n-1}=\dfrac{1}{256}\\ \Leftrightarrow\left(\dfrac{1}{2}\right)^{n-1}=\dfrac{1}{2^8}\\ \Leftrightarrow n-1=8\\ \Leftrightarrow n=9\)
Vậy \(\dfrac{3}{512}\) là số hạng thứ 9 của dãy.
BT
25 tháng 5 2017
a) Có \(u_n=\left(-3\right)^{2n-1}=\left(-3\right)^2.\left(-3\right)^{2n-3}\)\(=9.2^{2\left(n-1\right)-1}=9.u_{n-1}\)
Vì vậy \(\left(u_n\right)\) là dãy số nhân với \(u_1=\left(-3\right)^{2.1-1}=-3\) và \(q=9\).
b) Công thức truy hồi của dãy số \(\left(u_n\right)\) là \(u_n=9u_{n-1}\).
c) Có \(u_n=\left(-3\right)^{2n-1}=-19683=\left(-3\right)^9\)\(\Leftrightarrow2n-1=9\)\(\Leftrightarrow n=5\).
Vậy số hạng thứ 5 bằng \(-19683\).
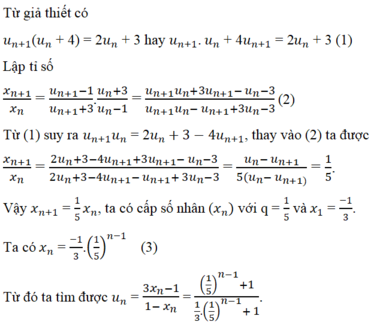
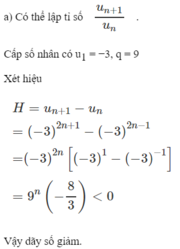
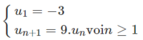
Cấp số nhân là 3
=> 1, 3, 9, 27, 81, 243, 729