Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét tgiac ABD và EBD có:
+ AB = BE
+ BD chung
+ góc ABD = EBD
=> Tgiac ABD = EBD (c-g-c)
=> đpcm
b) Tgiac ABD = EBD (cmt) => AD = DE (hai cạnh t/ứng)
Xét tgiac ADE có AD = DE => Tgiac ADE cân tại D
=> đpcm
c) AH \(\perp\)BC, DE\(\perp\)BC => AH\(//\)DE
=> góc HAE = AED (2 góc SLT do AH\(//\)DE)
Mà tgiac ADE cân tại D (cmt) => góc AED = DAE
=> góc HAE = DAE
=> AE là tia pgiac góc HAC (đpcm)
d) Xét tgiac ADK và EDC có:
+ góc DAK = DEC = 90o
+ góc ADK = EDC (2 góc đối đỉnh)
+ AD = DE (do tgiac ABD = EBD)
=> Tgiac ADK = EDC (g-c-g)
=> AK = EC và KD = DC (2 cạnh t/ứng)
=> Tgiac KDC cân tại K => Góc DCK = (180o- góc KDC) /2
Tgiac AED cân tại D => góc EAD = (180o- góc ADE) /2
Mà góc ADE = KDC (2 góc đối đỉnh) => góc DCK = EAD
Mà 2 góc này SLT => AE \(//\)KC
=> đpcm

4:
a: Xet ΔAMB và ΔAMC có
AM chung
MB=MC
AB=AC
=>ΔAMB=ΔAMC
b: Xet ΔAEM vuông tại E và ΔAFM vuông tại F có
AM chung
góc EAM=góc FAM
=>ΔAEM=ΔAFM
=>AE=AF
c: AE=AF
ME=MF
=>AM là trung trực của EF
mà K nằm trên trung trực của EF
nên A,M,K thẳng hàng

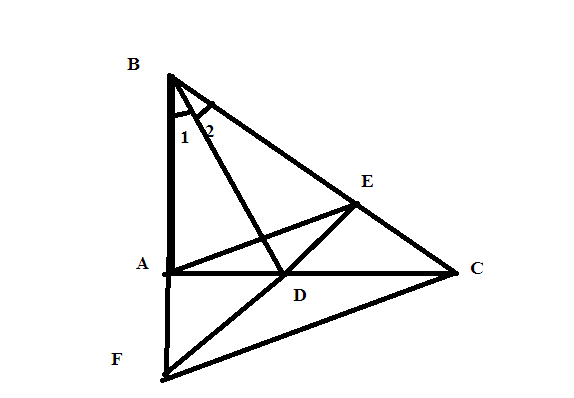
Xét ΔBAD và ΔBDE có:
BD là cạnh chung
B1=B2 (BD là tia phân giác của \(\widehat{B}\))
BA = BE (GT)
Nên ΔBAD= ΔBDE (c.g.c)
=>\(\widehat{ADB}=\widehat{BDE}\)
Ta có:\(\widehat{ADB}+\widehat{ADF}=\widehat{BDF}\)
\(\widehat{BDE}+\widehat{EDC}=\widehat{BDC}\)
Mà :\(\widehat{ADB}=\widehat{BDE}\)(CMT)
\(\widehat{ADF}=\widehat{EDC}\)( 2 góc đối đỉnh)
=>\(\widehat{BDF}=\widehat{BDC}\)
Xét ΔBDF và Δ BDC, có:
\(\widehat{BDF}=\widehat{BDC}\)
BD là cạnh chung
B1=B2
Nên ΔBDF=ΔBDC (g.c.g)
=>DC = DF
b)Ta có:ΔEDC vuông tại E=> DC là cạnh lớn nhất hay DC>DE
MÀ DE=AD (ΔBAD và ΔBDE)
=> AD< DC
c) Ta có BE=BA=>ΔBEA cân tại B
Mà BD là tia phân giác=>BD là đường trung trực
Vì :ΔBDF=ΔBDC=>BF=BC
=>ΔBFC cân tại B=>\(\widehat{C}=\widehat{F}\)
Ta có:\(\widehat{B}+\widehat{C}+\widehat{F}=180^o\)
=>\(\widehat{B}+\widehat{C}.2=180^O\)
=>\(\widehat{C}=\dfrac{180^O-\widehat{B}}{2}\)(1)
vÌ ΔBAE cân tại B
Tương tự ta có:
\(\widehat{E}=\dfrac{180^o-\widehat{B}}{2}\)(2)
Từ (1) và (2)=> \(\widehat{E}=\widehat{C}\)
Mà 2 góc này ở vị trí đồng vị=>AE // FC

a: Xét ΔBAD và ΔBED có
BA=BE
góc ABD=góc EBD
BD chung
=>ΔBAD=ΔBED
b: ΔBAD=ΔBED
=>góc BED=90 độ
=>DE vuông góc CB
c: BA=BE
DA=DE
=>BD là trung trực của AE
d: Xét ΔDAF vuông tại A và ΔDEC vuông tại E có
DA=DE
AF=EC
=>ΔDAF=ΔDEC
=>góc ADF=góc EDC
=>góc ADF+góc ADE=180 độ
=>F,D,E thẳng hàng
xét tam giác BAD và tam giác BED
BD chung
BA = BE
Góc B1=B2
=>tam giác BAD = tam giác BDE
=>DA = DE(hai cạnh tương ứng)
có A = E (2 góc tương ứng)
mà A =90°
=>E = 90°
=>DE vuông góc với BC
có BA = BE (chứng minh trên)
=>tam giác BAE cân
có BD là đường phân giác
=>BD cũng là đường cao
=>BD vuông góc với AE
xét tam giác ADF và tam giác EDC
Góc D1 = D2
DE = DA
=>tam giác ADF = tam giác EDC
=> AF = AC (hai cạnh tương ứng)
có BA + AF = BF, BE + EC= BC mà BA = BE, AF = EC
=>BF = BC
có tam giác BFC là tam giác cân
đường phân giác BD
=> BD cũng là đường trung trực của FC
=> M nằm trên đường trung trực BD
có DF = DC => D nằm trên đường trung trực BD
có BF = BC => B nằm trên đường trung trực BD
=> MDB thẳng hàng