PA
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TT
0
10 tháng 7 2021
a) Xét ΔAFC vuông tại F và ΔAFD vuông tại F có
AC=AD(=AB)
AF chung
Do đó: ΔAFC=ΔAFD(Cạnh huyền-cạnh góc vuông)
Suy ra: FC=FD(hai cạnh tương ứng)
mà C,F,D thẳng hàng(gt)
nên F là trung điểm của CD
Xét ΔBCD có
CA là đường trung tuyến ứng với cạnh BD(gt)
BF là đường trung tuyến ứng với cạnh DC(cmt)
CA cắt BF tại G(gt)
Do đó: G là trọng tâm của ΔBDC(Tính chất ba đường trung tuyến của tam giác)
\(\Leftrightarrow AG=\dfrac{1}{3}AC\)(Tính chất trọng tâm của tam giác)
mà \(AC=\dfrac{1}{2}BD\left(=AB\right)\)
nên \(AG=\dfrac{1}{3}\cdot\dfrac{1}{2}BD=\dfrac{1}{6}BD\)
hay BD=6AG(đpcm)
NQ
0
4 tháng 7 2017
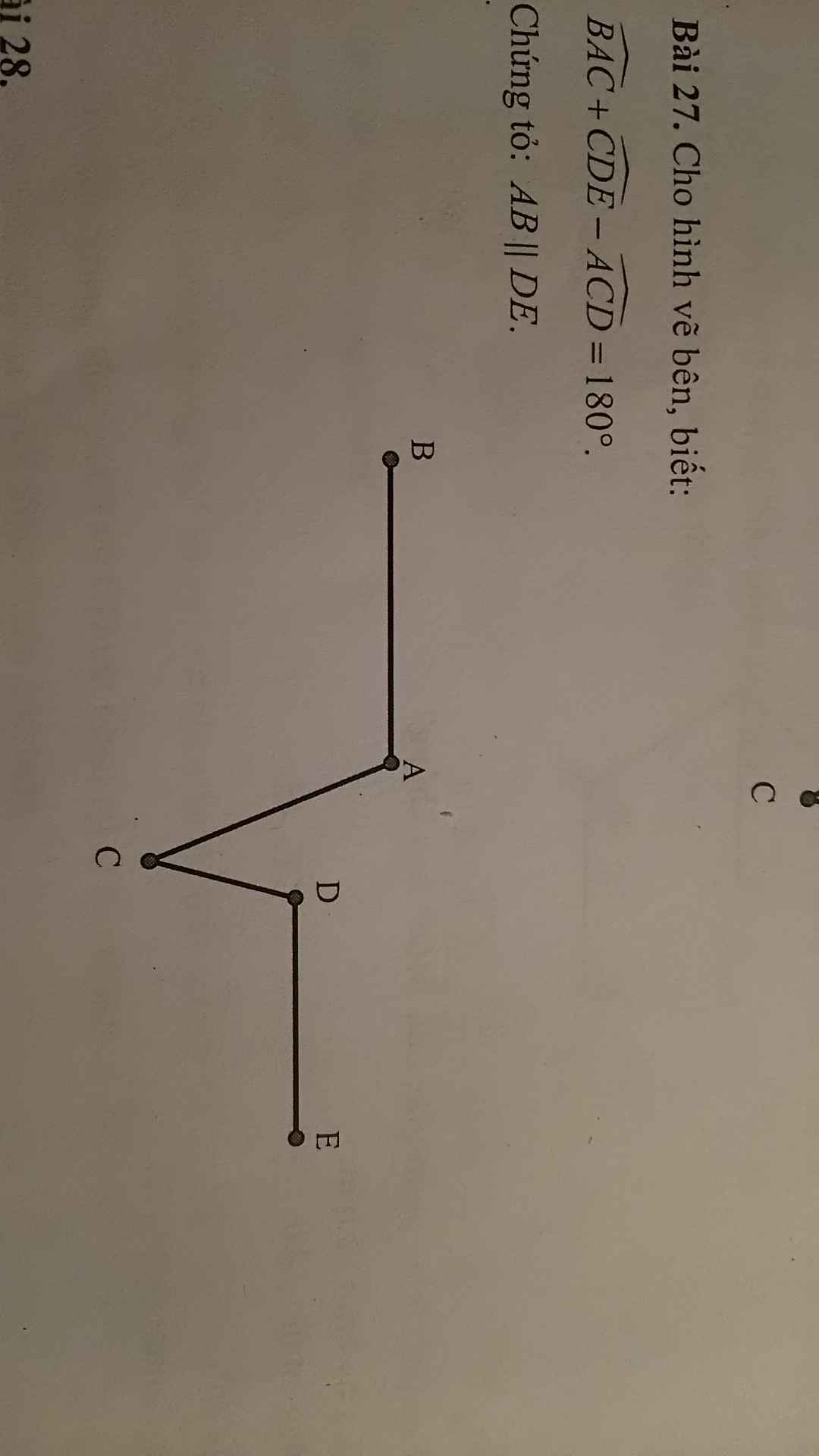
bạn cho đề thiếu thì phải vì nếu 2 góc BAC và ACD kề bù thì AB không song song với CD
Bạn xem lại đề đi
HB
24 tháng 2 2021
a, ΔABD có BA = BD (gt) và ˆABDABD^ = ˆABCABC^ = 60o60o
⇒ ΔABD đều (đpcm)
b, ΔABD đều ⇒ AB = AD
Xét ΔAHB và ΔAHD có:
AH chung; AB = AD (cmt); HB = HD (H là trung điểm của BD)
⇒ ΔAHB = ΔAHD (c.c.c)
⇒ ˆAHBAHB^ = ˆAHDAHD^ mà 2 góc này kề bù
⇒ ˆAHBAHB^ = ˆAHDAHD^ = 90o90o
⇒ AH ⊥ BD (đpcm)
c, ΔABD đều ⇒ AB = BD = AD = 2cm
⇒ HB = HD = 1cm
⇒ HC = BC - HB = 5 - 1 = 4cm
ΔAHB vuông tại H ⇒ AH = √AB2−HB2AB2−HB2 = √22−1222−12 = √33cm
ΔAHC vuông tại H ⇒ AC = √AH2+HC2AH2+HC2 = √3+423+42 = √1919cm
24 tháng 2 2021
a) Xét ΔBAD có BA=BD(gt)
nên ΔBAD cân tại B(Định nghĩa tam giác cân)
Xét ΔBAD cân tại B có \(\widehat{ABD}=60^0\)(gt)
nên ΔBAD đều(Dấu hiệu nhận biết tam giác đều)
b) Ta có: ΔBAD đều(cmt)
mà AH là đường trung tuyến ứng với cạnh BD(gt)
nên AH là đường cao ứng với cạnh BD(Định lí tam giác cân)
hay AH\(\perp\)BD(Đpcm)
