Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(1,4a=5b\Leftrightarrow\dfrac{a}{5}=\dfrac{b}{4}=\dfrac{b-a}{4-5}=\dfrac{27}{-1}=-27\\ \Leftrightarrow\left\{{}\begin{matrix}a=-135\\b=-108\end{matrix}\right.\\ 2,\dfrac{1}{3}x=\dfrac{1}{2}y=\dfrac{1}{5}z\Leftrightarrow\dfrac{x}{3}=\dfrac{y}{2}=\dfrac{z}{5}=\dfrac{x+2y-z}{3+4-5}=\dfrac{8}{2}=4\\ \Leftrightarrow\left\{{}\begin{matrix}x=12\\y=8\\z=20\end{matrix}\right.\\ 3,\dfrac{1}{3}a=\dfrac{1}{2}b;\dfrac{1}{5}a=\dfrac{1}{7}c\\ \Leftrightarrow\dfrac{a}{15}=\dfrac{b}{10}=\dfrac{c}{21}=\dfrac{a+b+c}{15+10+21}=\dfrac{184}{46}=4\\ \Leftrightarrow\left\{{}\begin{matrix}a=60\\b=40\\c=84\end{matrix}\right.\)

Theo bài ra, ta có:
\(\frac{1}{2}a=\frac{1}{5}b=\frac{1}{7}c\Rightarrow\frac{a}{2}=\frac{b}{5}=\frac{c}{7}\)
Áp dụng tích chất của dãy tỉ số bằng nhau, ta có:
\(\frac{a}{2}=\frac{b}{5}=\frac{c}{7}=\frac{2c}{14}=\frac{a+b-2c}{2+5-14}=\frac{70}{-7}=-10\)
\(\Rightarrow\hept{\begin{cases}a=-10.2=-20\\b=-10.5=-50\\c=-10.7=-70\end{cases}}\)

vì a,b,c tỉ lệ nghịch với 1/2;1/5;1/7 nên a/2=b/5=c/7. Hay a/2=b/5=2c/14
ADTCCDTSBN TA CÓ
a/2=b/5=2c/14=a+b-2c/2+5-14=70/-7=-10
Suy ra a/2=-10 nên a=-20
b/5=-10 nên b=-50
2c/14=-10 nên c=-70
Biết 3 số a,b,c chúng tỉ lệ nghịch với 1/2 ; 1/5 ; 1/7
=> a/2 = b/5 = c/7
=> a/2 = b/5 = -2c/-14
Áp dụng tc dãy tỉ số = nhau ta đc :
a/2 = b/5 = -2c/-14 = (a+b-2c)/(2+5-14) = 70/-7 = -10
=>a= -20 ; b= -50 ; c = -70
=> a+b-c = 0

do a,b tỉ lệ nghịch với \(\frac{1}{3};\frac{1}{2}\); a, c tỉ lệ nghịch với \(\frac{1}{5};\frac{1}{7}\)nên ta có:
\(\frac{b}{2}=\frac{a}{3};\frac{a}{5}=\frac{c}{7}\Rightarrow\frac{b}{1\text{0}}=\frac{a}{15}=\frac{c}{21}\)
theo đề bài và tính chất của dãy tỉ số bằng nhau ta có:
\(\frac{a}{15}=\frac{b}{1\text{0}}=\frac{c}{21}=\frac{a+b+c}{15+1\text{0}+21}=\frac{184}{46}=4\)
vậy a= 4.15= 60; b= 4.10= 40; c= 4.21= 84
các bạn tự kết luận nhé

Bài làm
Gọi số đo của ba góc A, B, C lần lượt là x, y, z
Mà số đo của các góc lần lượt tỉ lệ với \(\frac{1}{2};\frac{1}{3};\frac{2}{5}\)
=> \(x.\frac{1}{2}.\frac{1}{30}\)= \(x.\frac{1}{3}.\frac{1}{30}\)=\(x.\frac{2}{5}.\frac{1}{30}\)
=> \(\frac{x}{60}\)= \(\frac{y}{90}\)= \(\frac{z}{75}\)
Vì theo định lí, tổng ba góc của tam giác là 180o
=> x + y + z = 180o
Áp dụng tính chất dãy tỉ số bằng nhau:
Ta có: \(\frac{x}{60}=\frac{y}{90}=\frac{z}{75}=\frac{x+y+z}{60+90+75}=\frac{180}{225}=\frac{36}{45}=\frac{4}{5}\)
Do đó: \(\hept{\begin{cases}\frac{x}{60}=\frac{4}{5}\\\frac{y}{90}=\frac{4}{5}\\\frac{z}{75}=\frac{4}{5}\end{cases}}\Rightarrow\hept{\begin{cases}x=48\\y=72\\z=60\end{cases}}\)
Vậy độ dài của góc A là 48o
độ dài của góc B là 72o
độ dài của góc C là 60o
# Chúc bạn học tốt #

Vì các số a,b,c tỉ lệ nghịch với \(\frac{1}{2};\frac{1}{3};\frac{1}{4}\)nên
\(a:2=b:3=c:4\Rightarrow\frac{a}{2}=\frac{b}{3}=\frac{c}{4}\)
Đặt \(\frac{a}{2}=\frac{b}{3}=\frac{c}{4}=k\)nên \(a=2k;b=3k;c=4k\)
Khi đó \(M=\frac{\left(2a+3b+4c\right)^2}{a^2+b^2+c^2}=\frac{\left(2.2k+3.3k+4.4k\right)^2}{\left(2k\right)^2+\left(3k\right)^2+\left(4k\right)^2}\)
\(M=\frac{\left(4k+9k+16k\right)^2}{4k^2+9k^2+16k^2}\)
\(M=\frac{\left[k.\left(4+9+16\right)\right]^2}{k^2.\left(4+9+16\right)}\)
\(M=\frac{k^2.29^2}{k^2.29}=29\)
Vậy \(M=29\)
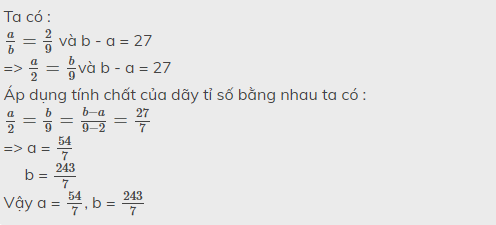
Vì a,b tỉ lệ nghịch với \(\frac{1}{3};\frac{1}{2}\) suy ra \(\frac{a}{3}=\frac{b}{2}\Rightarrow\frac{a}{15}=\frac{b}{10}\) (1)
a,c tỉ lệ nghịch với \(\frac{1}{5};\frac{1}{7}\) suy ra \(\frac{a}{5}=\frac{c}{7}\Rightarrow\frac{a}{15}=\frac{c}{21}\) (2)
Từ (1) và (2) suy ra \(\frac{a}{15}=\frac{b}{10}=\frac{c}{21}\). Áp dụng tc dãy tỉ số bằng nhau ta có:
\(\frac{a}{15}=\frac{b}{10}=\frac{c}{21}=\frac{a+b+c}{15+10+21}=\frac{184}{46}=4\)
\(\Rightarrow\begin{cases}\frac{a}{15}=4\Rightarrow a=4\cdot15=60\\\frac{b}{10}=4\Rightarrow b=4\cdot10=40\\\frac{c}{21}=4\Rightarrow c=4\cdot21=84\end{cases}\)
\(\Rightarrow M=a^2+b^2-c^2=60^2+40^2-84^2=-1856\)
-1856