
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: \(\cos\alpha=\dfrac{1}{2}\)
\(\tan\alpha=\sqrt{3}\)
\(\cot\alpha=\dfrac{\sqrt{3}}{3}\)

a, Tìm được sinα = 24 5 , tanα = 24 , cotα = 1 24
b, cosα = 5 3 , tanα = 2 5 , cotα = 5 2
c, sinα = ± 2 5 , cosα = ± 1 5 , cotα = 1 2
d, sinα = ± 1 10 , cosα = ± 3 10 , tanα = 1 3

Cho α là góc nhọn, sinα = 1/2. Tính cosα; tanα; cotα
Ta có: sin 2 α + cos 2 α = 1
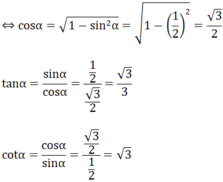

b)
Có: \(cot\alpha=\dfrac{cos\alpha}{sin\alpha}\)
Vì $\alpha $ là góc nhọn nên `0<sin\alpha<1`
\(\Rightarrow\dfrac{cos\alpha}{sin\alpha}>\dfrac{cos\alpha}{1}=cos\alpha\)
Vậy \(cos\alpha< cot\alpha\)

Dựng một tam giác vuông ta có:
a, Độ dài cạnh góc vuông là 3, cạnh huyền là 5, góc đối diện với cạnh góc vuông đó là góc α
b, Độ dài cạnh góc vuông là 4, cạnh huyền là 7,góc giữa cạnh góc vuông và cạnh huyền đó là góc α
c, Độ dài hai cạnh góc vuông là 3 và 2, góc đối diện với cạnh góc vuông độ dài 3 là góc α
d, Độ dài hai cạnh góc vuông là 5 và 6, góc đối diện với cạnh góc vuông độ dài 6 là góc α

\(1+tan^2a=\dfrac{1}{cos^2a}=1:\dfrac{1}{25}=25\)
=>tan^2a=24
=>tana=2*căn 6
\(cota=\dfrac{1}{2\sqrt{6}}=\dfrac{\sqrt{6}}{12}\)
\(sina=\sqrt{1-\left(\dfrac{1}{5}\right)^2}=\dfrac{2\sqrt{6}}{5}\)
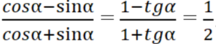
Bạn nên nhớ \(\sin^2\alpha+\cos^2\alpha=1\)
Lại thêm \(\cos\alpha-\sin\alpha=\dfrac{1}{5}\Leftrightarrow\sin\alpha=\cos\alpha-\dfrac{1}{5}\) nên ta có \(\left(\cos\alpha-\dfrac{1}{5}\right)^2+\cos^2\alpha=1\) \(\Leftrightarrow\cos^2\alpha-\dfrac{2}{5}\cos\alpha+\dfrac{1}{25}+\cos^2\alpha-1=0\)
\(\Leftrightarrow2\cos^2\alpha-\dfrac{2}{5}\cos\alpha-\dfrac{24}{25}=0\)
\(\Leftrightarrow\cos^2\alpha-\dfrac{1}{5}\cos\alpha-\dfrac{12}{25}=0\)
\(\Leftrightarrow25\cos^2\alpha-5\cos\alpha-12=0\)
Đặt \(\cos\alpha=p\left(0< p< 1\right)\) thì ta có \(25p^2-5p-12=0\)
Ta có \(\Delta=\left(-5\right)^2-4.25\left(-12\right)=1225>0\), vậy:
\(x_1=\dfrac{-\left(-5\right)+\sqrt{1225}}{2.25}=\dfrac{4}{5}\left(nhận\right)\)
\(x_2=\dfrac{-\left(-5\right)-\sqrt{1225}}{2.25}=-\dfrac{3}{5}\left(loại\right)\)
Vậy ta có \(\cos\alpha=\dfrac{4}{5}\). Ta lại có \(\sin\alpha=\cos\alpha-\dfrac{1}{5}=\dfrac{4}{5}-\dfrac{1}{5}=\dfrac{3}{5}\)
Mà \(\cot\alpha=\dfrac{\cos\alpha}{\sin\alpha}=\dfrac{\dfrac{4}{5}}{\dfrac{3}{5}}=\dfrac{4}{3}\). Vậy \(\cot\alpha=\dfrac{4}{3}\)