Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C.
Ta có
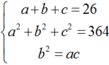
Từ đó ta có
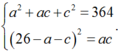
Đặt 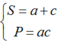 có hệ
có hệ
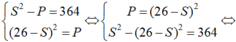
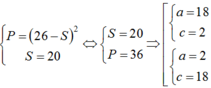
Vậy b2 = ac = 36 nên b = 6.

Giả sử \(c\le1\).
Khi đó: \(ab+bc+ca-abc=ab\left(1-c\right)+c\left(a+b\right)\ge0\)
\(\Rightarrow ab+bc+ca\ge abc\left(1\right)\)
Đẳng thức xảy ra chẳng hạn với \(a=2,b=c=0\).
Theo giả thiết:
\(4=a^2+b^2+c^2+abc\ge2ab+c^2+abc\)
\(\Leftrightarrow ab\left(c+2\right)\le4-c^2\)
\(\Leftrightarrow ab\le2-c\)
Trong ba số \(\left(a-1\right),\left(b-1\right),\left(c-1\right)\) luôn có hai số cùng dấu.
Không mất tính tổng quát, giả sử \(\left(a-1\right)\left(b-1\right)\ge0\).
\(\Rightarrow ab-a-b+1\ge0\)
\(\Leftrightarrow ab\ge a+b-1\)
\(\Leftrightarrow abc\ge ca+bc-c\)
\(\Rightarrow abc+2\ge ca+bc+2-c\ge ab+bc+ca\left(2\right)\)
Từ \(\left(1\right)\) và \(\left(2\right)\Rightarrow\) Bất đẳng thức được chứng minh.

Chọn C
Để a; b; c theo thứ tự lập thành cấp số cộng khi và chỉ khi
b − a = c − b ⇔ b − a 2 = c − b 2 ⇔ b 2 − 2 a b + a 2 = c 2 − 2 b c + b 2 ⇔ a 2 − c 2 = 2 a b − 2 b c
⇔ a 2 + c 2 = 2 c 2 + 2 a b − 2 b c = 2 a b + 2 c c − b = 2 a b + 2 c b − a = 2 a b + 2 b c − 2 a c

Chọn B
Để 3 số a, b, c theo thứ tự lập thành cấp số cộng khi và chỉ khi:
b − a = c − b ⇔ b − a 2 = c − b 2 ⇔ b 2 − 2 a b + a 2 = c 2 − 2 b c + b 2 ⇔ a 2 − c 2 = 2 a b − 2 b c .
Suy ra chọn đáp án B.
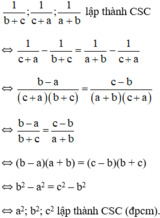
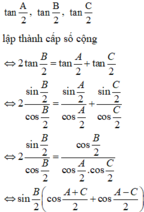
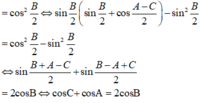



Chọn C.
Do a; b; c theo thứ tự lập thành cấp số cộng khi và chỉ khi b – a = c – b
⇔ (b – a)2 = (c – b)2 ⇔ a2 – c2 = 2ab – 2bc
⇔ a2 +c2 = 2c2 + 2ab – 2bc = 2ab + 2c(c – b) = 2ab + 2c(b – a) = 2ab + 2bc – 2ac.