Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ba số \(\frac{2}{{b - a}},\frac{1}{b},\frac{2}{{b - c}}\) theo thứ tự lập thành cấp số cộng nên ta có:
\(\begin{array}{l}\frac{2}{{b - a}} + \frac{2}{{b - c}} = 2.\frac{1}{b} \Leftrightarrow \frac{1}{{b - a}} + \frac{1}{{b - c}} = \frac{1}{b} \Leftrightarrow \frac{{\left( {b - c} \right) + \left( {b - a} \right)}}{{\left( {b - a} \right)\left( {b - c} \right)}} = \frac{1}{b}\\ \Leftrightarrow \frac{{b - c + b - {\rm{a}}}}{{{b^2} - ab - bc + ac}} = \frac{1}{b} \Leftrightarrow \frac{{2b - c - {\rm{a}}}}{{{b^2} - ab - bc + ac}} = \frac{1}{b} \Leftrightarrow b\left( {2b - c - {\rm{a}}} \right) = {b^2} - ab - bc + ac\\ \Leftrightarrow 2{b^2} - bc - {\rm{ab}} = {b^2} - ab - bc + ac \Leftrightarrow {b^2} = {\rm{a}}c\end{array}\).
Vậy ba số \(a,b,c\) theo thứ tự lập thành cấp số nhân.

Chọn C
Để a; b; c theo thứ tự lập thành cấp số cộng khi và chỉ khi
b − a = c − b ⇔ b − a 2 = c − b 2 ⇔ b 2 − 2 a b + a 2 = c 2 − 2 b c + b 2 ⇔ a 2 − c 2 = 2 a b − 2 b c
⇔ a 2 + c 2 = 2 c 2 + 2 a b − 2 b c = 2 a b + 2 c c − b = 2 a b + 2 c b − a = 2 a b + 2 b c − 2 a c

Chọn C.
Do a; b; c theo thứ tự lập thành cấp số cộng khi và chỉ khi b – a = c – b
⇔ (b – a)2 = (c – b)2 ⇔ a2 – c2 = 2ab – 2bc
⇔ a2 +c2 = 2c2 + 2ab – 2bc = 2ab + 2c(c – b) = 2ab + 2c(b – a) = 2ab + 2bc – 2ac.

Chọn D
Ta có A=(a-c)2+(b-c)2+(b-d)2-(a-d)2=(a-aq2 )2+(aq-aq2 )2+(aq-aq3)2-(a-aq3)2=0

Theo giả thiết ta có : \(\cot A+\cot C=2\cot B\)
\(\Leftrightarrow\frac{\sin\left(A+C\right)}{\sin A\sin C}=\frac{2\cos B}{\sin B}\)
\(\Leftrightarrow\sin^2B=2\sin B\sin C\cos B=\left[\cos\left(A-C\right)-\cos\left(A+C\right)\right]\cos B\)
\(\Leftrightarrow\sin^2B=\cos\left(A-C\right)\cos B-\cos\left(A+C\right)\cos B=-\cos\left(A-C\right)\cos\left(A+C\right)+\cos^2B\)
\(\Leftrightarrow\sin^2B=-\frac{1}{2}\left(\cos2A+\cos2C\right)+1-\sin^2B=-\frac{1}{2}\left(1-2\sin^2A+1-2\sin^2C\right)+1-\sin^2B\)
\(\Rightarrow2\sin^2B=\sin^2A+\sin^2C\Leftrightarrow2b^2=a^2+c^2\)
Vậy chứng tỏ \(a^2,b^2,c^2\) theo thứ tự đó cũng lập thành một cấp số cộng

\(a,b,c\) lập thành CSN nên \(b^2=ac\)
Ta có \(VT=\left(a+c\right)^2-b^2\)
\(=a^2+2ac+c^2-ac\)
\(=a^2+ac+c^2\)
\(=a^2+b^2+c^2\)
\(=VP\)
Vậy đẳng thức được chứng minh.
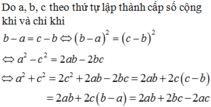
Chọn B
Để 3 số a, b, c theo thứ tự lập thành cấp số cộng khi và chỉ khi:
b − a = c − b ⇔ b − a 2 = c − b 2 ⇔ b 2 − 2 a b + a 2 = c 2 − 2 b c + b 2 ⇔ a 2 − c 2 = 2 a b − 2 b c .
Suy ra chọn đáp án B.