NN
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
QT
Quoc Tran Anh Le
Giáo viên
22 tháng 9 2023
Ba số \(\frac{2}{{b - a}},\frac{1}{b},\frac{2}{{b - c}}\) theo thứ tự lập thành cấp số cộng nên ta có:
\(\begin{array}{l}\frac{2}{{b - a}} + \frac{2}{{b - c}} = 2.\frac{1}{b} \Leftrightarrow \frac{1}{{b - a}} + \frac{1}{{b - c}} = \frac{1}{b} \Leftrightarrow \frac{{\left( {b - c} \right) + \left( {b - a} \right)}}{{\left( {b - a} \right)\left( {b - c} \right)}} = \frac{1}{b}\\ \Leftrightarrow \frac{{b - c + b - {\rm{a}}}}{{{b^2} - ab - bc + ac}} = \frac{1}{b} \Leftrightarrow \frac{{2b - c - {\rm{a}}}}{{{b^2} - ab - bc + ac}} = \frac{1}{b} \Leftrightarrow b\left( {2b - c - {\rm{a}}} \right) = {b^2} - ab - bc + ac\\ \Leftrightarrow 2{b^2} - bc - {\rm{ab}} = {b^2} - ab - bc + ac \Leftrightarrow {b^2} = {\rm{a}}c\end{array}\).
Vậy ba số \(a,b,c\) theo thứ tự lập thành cấp số nhân.
CM
8 tháng 1 2019
Chọn D
Ta có A=(a-c)2+(b-c)2+(b-d)2-(a-d)2=(a-aq2 )2+(aq-aq2 )2+(aq-aq3)2-(a-aq3)2=0
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 1 2022
Do a;b;c;d là 1 cấp số nhân \(\Rightarrow\left\{{}\begin{matrix}ad=bc\\ac=b^2\\bd=c^2\end{matrix}\right.\)
\(\left(b-c\right)^2+\left(c-a\right)^2+\left(d-b\right)^2\)
\(=b^2+c^2-2bc+c^2+a^2-2ca+d^2+b^2-2bd\)
\(=ac+bd-2ad+bd+a^2-2ca+d^2+ac-2bd\)
\(=a^2-2ab+d^2=\left(a-d\right)^2\)
CM
1 tháng 8 2017
Chọn D
Theo tính chất cấp số nhân, Ta có: ac=2/3 b2. Theo hệ thức lượng trong tam giác vuông, Ta có: b=a.sinB, c=a.cosB. vậy Ta có
5 tháng 1 2021
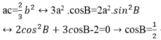
3: Ta có \(\dfrac{1}{u_{n+1}}=\dfrac{1}{u_n}-1\).
Do đó \(\dfrac{1}{u_{100}}=\dfrac{1}{u_{99}}-1=\dfrac{1}{u_{98}}-2=...=\dfrac{1}{u_1}-99=\dfrac{1}{-2}-99=\dfrac{-199}{2}\Rightarrow u_{100}=\dfrac{-2}{199}\).
CM
7 tháng 12 2019
Chọn C.
Ta có
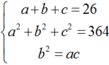
Từ đó ta có
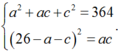
Đặt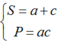 
có hệ
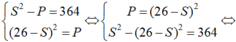
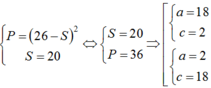
Vậy b2 = ac = 36 nên b = 6.
\(a,b,c\) lập thành CSN nên \(b^2=ac\)
Ta có \(VT=\left(a+c\right)^2-b^2\)
\(=a^2+2ac+c^2-ac\)
\(=a^2+ac+c^2\)
\(=a^2+b^2+c^2\)
\(=VP\)
Vậy đẳng thức được chứng minh.