NA
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
24 tháng 3 2022
\(a< b\)
\(\Leftrightarrow2a< 2b\)
\(a< b\)
\(\Leftrightarrow a+a< b+a\)
\(\Leftrightarrow2a< a+b\)
\(a< b\)
\(\Leftrightarrow-1a>-1b\)
\(\Leftrightarrow-a>-b\)
PT
1
CM
22 tháng 2 2018
+ a < b ⇒ 2a < 2b (nhân cả hai vế với 2 > 0, BĐT không đổi chiều).
+ a < b ⇒ a + a < b + a (Cộng cả hai vế với a)
hay 2a < a + b.
+ a < b ⇒ (-1).a > (-1).b (Nhân cả hai vế với -1 < 0, BĐT đổi chiều).
hay –a > -b.
TG
1
29 tháng 3 2023
a: a>b
=>3a>3b
=>3a+5>3b+5
b: a>b
=>2a>2b
=>2a-3>2b-3>2b-4
PT
1
MP
24 tháng 4 2023
1.
a. -3a - 1 + 1 > -3b - 1 + 1 (cộng cả 2 vế cho 1)
-3a . \(\left(\dfrac{-1}{3}\right)\) < -3b . \(\left(\dfrac{-1}{3}\right)\) (nhân cả vế cho \(\dfrac{-1}{3}\) )
a < b
b. 4a + 3 + (- 3) < 4b + 3 +(- 3) (cộng cả 2 vế cho -3)
4a . \(\dfrac{1}{4}\) < 4b . \(\dfrac{1}{4}\) (nhân cả 2 vế cho \(\dfrac{1}{4}\) )
a < b
2.
a. Ta có: a < b
3a < 3b ( nhân cả 2 vế cho 3)
3a - 7 < 3b - 7 (cộng cả 2 vế cho - 7 )
b. Ta có: a < b
-2a > -2b (nhân cả 2 vế cho -2)
5 - 2a > 5 - 2b ( cộng cẩ 2 vế cho 5)
c. Ta có: a < b
2a < 2b (nhân cả vế cho 2)
2a + 3 < 2b + 3 (cộng cả 2 vế cho 3)
d. Ta có: a < b
3a < 3b (nhân cả 2 vế cho 3)
3a - 4 < 3b - 4 (cộng cả 2 vế cho -4)
Ta có: 3 < 4
đến đây ko bắt cầu qua đc chắc đề bài sai
NN
20 tháng 4 2020
Ta có: \(a+b=a+b\)
Vì \(a>b\)( giả thiết )
\(\Rightarrow a+b+a>a+b+b\)\(\Rightarrow2a+b>a+2b\)
hay \(2b+a< 2a+b\)
VC
Vũ Cao Minh⁀ᶦᵈᵒᶫ ( ✎﹏IDΣΛ亗 )
CTV
VIP
20 tháng 4 2020
Trừ hai biểu thức cho nhau là ra ý mà
Xét hiệu \(\left(2b+a\right)-\left(2a+b\right)=b+b+a-a-a-b\)
\(=\left(b+b-b\right)-\left(a+a-a\right)=b-a\). Mà \(a>b\Leftrightarrow b< a\)
\(\Rightarrow b-a< 0\) hay \(2b+a< 2a+b\)
SG
2
22 tháng 4 2017
Ta có:
a < b và 2 > 0 => 2a < 2b
a < b cộng hai vế với a
=> a + a < a + b => 2a < a + b
a < b và -1 < 0 => -a > -b
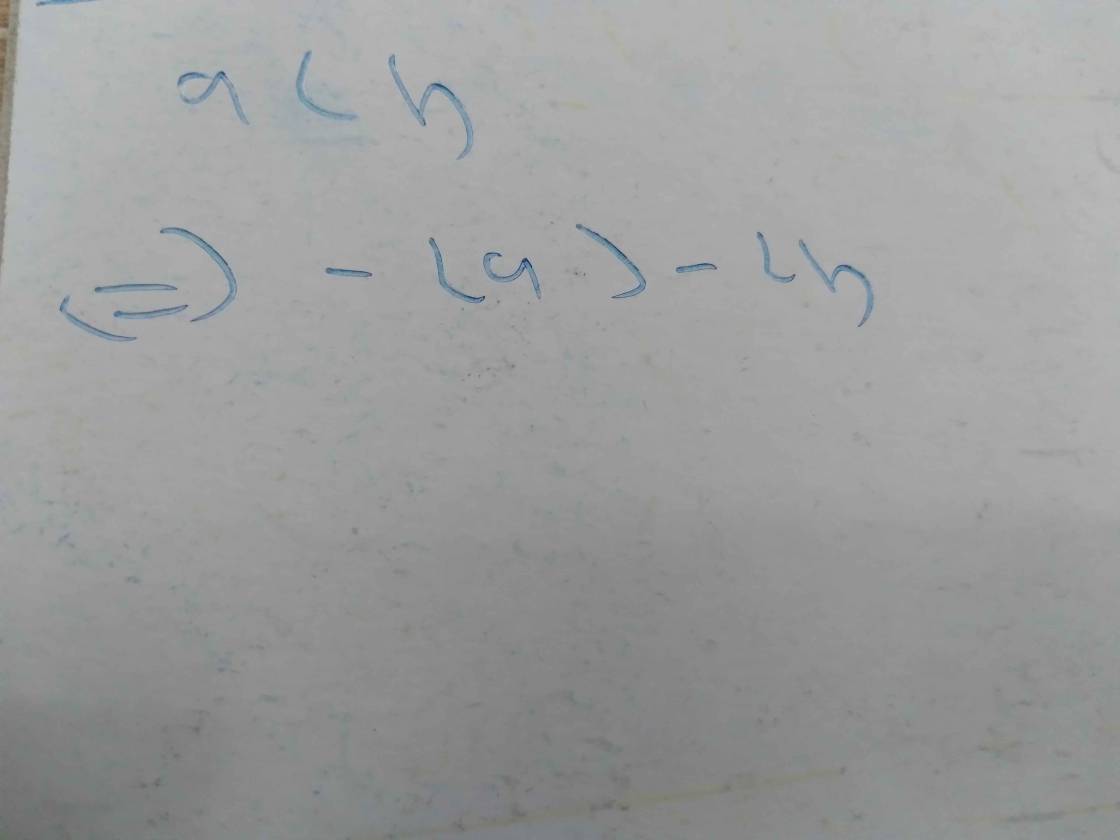
1.Vì a < b nên a-b sẽ bằng một số nguyên âm.
Vậy a-b < 0.
2.Vì a < b nên 2a < 2b.
2a=a.a:nếu a+b=số nguyên dương thì 2a > a+b mà nếu a+b=số nguyên âm thì 2a > a+b.
2b=b.b:nếu a+b=số nguyên dương thì 2b > a+b mà nếu a+b=số nguyên âm thì 2b > a+b.