NT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
26 tháng 1 2022
\(A=4+4^2+4^3+...+4^{81}=4\left(1+4+4^2\right)+...+4^{79}\left(1+4+4^2\right)\)
\(=21\left(4+...+4^{79}\right)⋮21\)vậy ta có đpcm
NM
1
17 tháng 12 2023
CM: A ⋮ 5
A = 1 + 4 + 42 + 43 + ... + 460
A = (1 + 4) + (42 + 43) + ... + (459 + 460)
A = 5 + 42 . (1 + 4) + ... + 459 . (1 + 4)
A = 5 + 42 . 5 + ... + 459 . 5
A = 5 . (1 + 42 + ... + 459) ⋮ 5
Vậy A ⋮ 5
CM: A ⋮ 21
A = 1 + 4 + 42 + 43 + ... + 460
A = (1 + 4 + 42) + (43 + 44 + 45) + ... + (458 + 459 + 460)
A = 21 + 43 . (1 + 4 + 42) + ... + 458 . (1 + 4 + 42)
A = 21 + 43 . 21 + ... + 458 . 21
A = 21 . (1 + 43 + ... + 458) ⋮ 21
Vậy A ⋮ 21
NT
0
NT
3
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
7 tháng 1
A = 1 + 4 + 42 + 43 + ... + 42021
A = 40 + 41 + 42 + 43 +...+ 42021
Xét dãy số 0; 1; 2; 3;...; 2021
Dãy số trên có số số hạng là:
(2021 - 0) : 1 + 1 = 2022
Vậy A có 2022 số hạng
vì 2022 : 3 = 674
Vậy ta nhóm 3 số hạng liên tiếp của A thành một nhóm thì khi đó
A = (1 + 4 + 42) + (43 + 44 + 45) +...+ (42019 + 42020 + 42021)
A = (1 + 4 + 16) + 43.(1 + 4 + 42) + ... +42019.(1 + 4 + 42)
A = 21 + 43.21 +... + 42019.21
A = 21.(1 + 43 + ... + 42019)
21 ⋮ 21 ⇒ 21.(1 + 43 + ...+ 42019) ⋮ 21 ⇒ A ⋮ 21 (đpcm)
NM
Nguyễn Minh Quang
Giáo viên
11 tháng 12 2021
ta có
\(1+3+3^2+..+3^{2000}=\left(1+3+3^2\right)+\left(3^3+3^4+3^5\right)+..+\left(3^{1998}+3^{1999}+3^{2000}\right)\)
\(=13.1+13\cdot3^3+..+13\cdot3^{1998}\) chia hết cho 13
tương tự
\(1+4+4^2+..+4^{2012}=\left(1+4+4^2\right)+..+\left(4^{2010}+4^{2011}+4^{2012}\right)\)
\(=21.1+21\cdot4^3+..+21.4^{2010}\) chia hết cho 21
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
1 tháng 8 2023
Bài 1:
\(2^{49}=\left(2^7\right)^7=128^7;5^{21}=\left(5^3\right)^7=125^7\\ Vì:128^7>125^7\Rightarrow2^{49}>5^{21}\)
Bài 2:
\(a,S=1+3+3^2+3^3+...+3^{99}\\ =\left(1+3+3^2+3^3\right)+3^4.\left(1+3+3^2+3^3\right)+...+3^{96}.\left(1+3+3^2+3^3\right)\\ =40+3^4.40+...+3^{96}.40\\ =40.\left(1+3^4+...+3^{96}\right)⋮40\\ b,S=1+4+4^2+4^3+...+4^{62}\\ =\left(1+4+4^2\right)+4^3.\left(1+4+4^2\right)+...+4^{60}.\left(1+4+4^2\right)\\ =21+4^3.21+...+4^{60}.21\\ =21.\left(1+4^3+...+4^{60}\right)⋮21\)
1 tháng 8 2023
Bài 1 :
\(2^{49}=\left(2^7\right)^7=128^7\)
\(5^{21}=\left(5^3\right)^7=125^7\)
mà \(125^7< 128^7\)
\(\Rightarrow2^{49}>5^{21}\)
Bài 2 :
a) \(S=1+3+3^2+3^3+...3^{99}\)
\(\Rightarrow S=\left(1+3+3^2+3^3\right)+3^4\left(1+3+3^2+3^3\right)...+3^{96}\left(1+3+3^2+3^3\right)\)
\(\Rightarrow S=40+40.3^4+...+40.3^{96}\)
\(\Rightarrow S=40\left(1+3^4+...+3^{96}\right)⋮40\)
\(\Rightarrow dpcm\)
b) \(S=1+4+4^2+4^3+...4^{62}\)
\(\Rightarrow S=\left(1+4+4^2\right)+4^3\left(1+4+4^2\right)+...4^{60}\left(1+4+4^2\right)\)
\(\Rightarrow S=21+4^3.21+...4^{60}.21\)
\(\Rightarrow S=21\left(1+4^3+...4^{60}\right)⋮21\)
\(\Rightarrow dpcm\)
PT
1
CM
21 tháng 11 2019
D = 1 + 4 + 4 2 + 4 3 + . . . + 4 58 + 4 59
= 1 + 4 + 4 2 + 4 3 + 4 4 + 4 5 + ... + 4 57 + 4 58 + 4 59
= 1 + 4 + 4 2 + 4 3 . 1 + 4 + 4 2 + ... + 4 57 . 1 + 4 + 4 2
= 21 + 21 . 4 3 + . . . + 21 . 4 57 ⋮ 21
PT
1
VN
Võ Ngọc Phương
VIP
31 tháng 10 2023
Đặt \(A=4+4^2+4^3+...+4^{89}+4^{90}\)
Ta có: \(A=\left(4+4^2+4^3\right)+...+\left(4^{88}+4^{89}+4^{90}\right)\)
\(A=84+...+4^{87}.\left(4+4^2+4^3\right)\)
\(A=84+...+4^{87}.84\)
\(A=84.\left(1+...+4^{87}\right)\)
Vì \(84⋮21\) nên \(84.\left(1+...+4^{87}\right)⋮21\)
Vậy \(A⋮21\)
\(#\) Hallowen vui vẻ 🎃
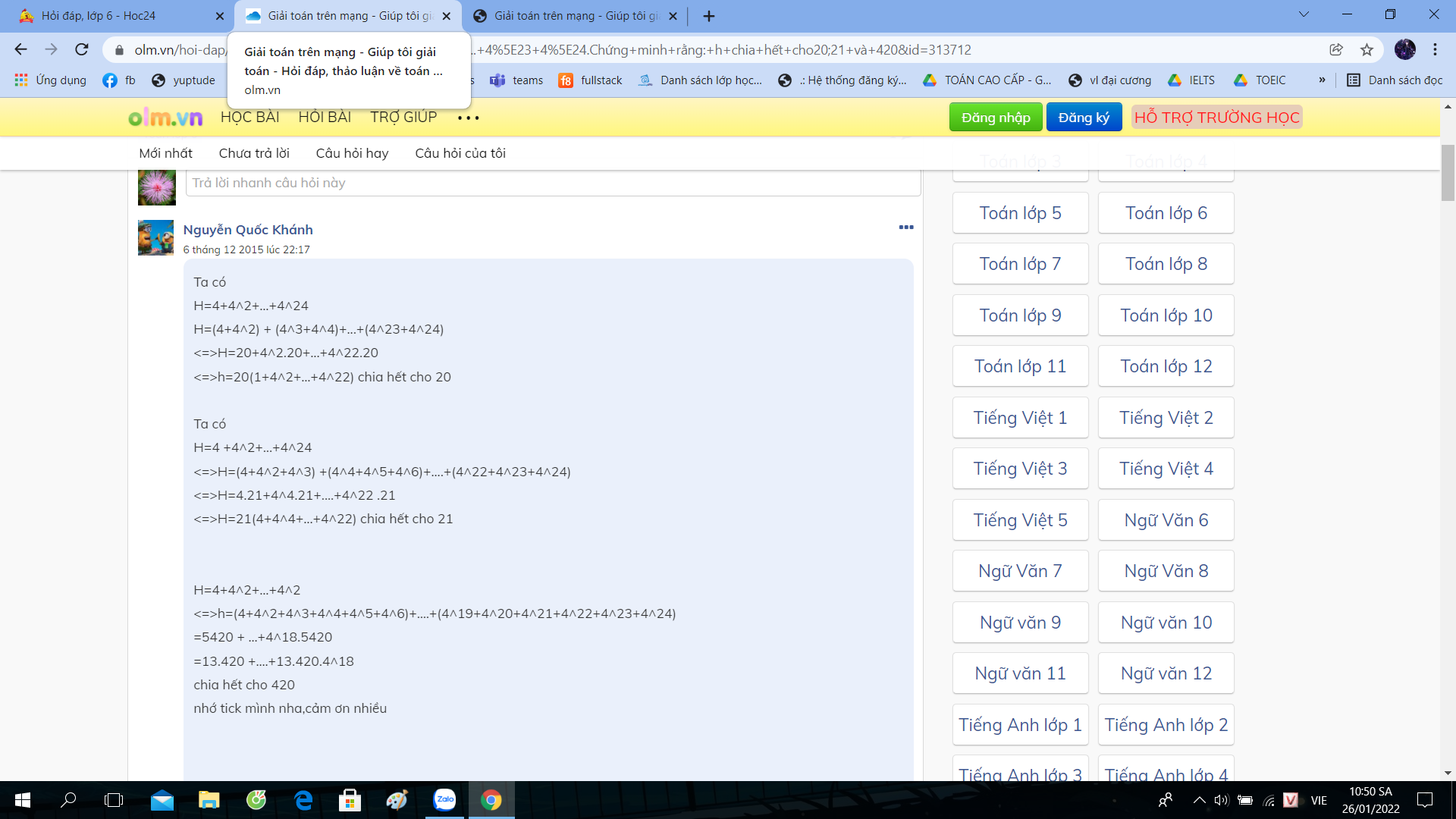
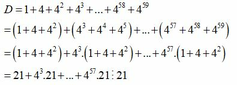
Ta có: A=1+4+42+…+42012
=>A=(1+4+42)+…+(42010+42011+42012)
=>A=1.(1+4+42)+…+42010.(1+4+42)
=>A=1.21+…+42010.21
=>A=(1+…+42010).21 chia hết cho 21
Vậy A chia hết cho 21