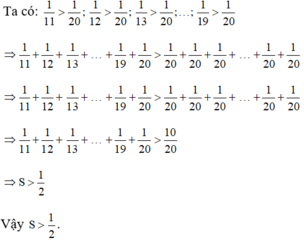Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(a,A=\dfrac{\left(119+1\right)\left(119-1+1\right)}{2}=\dfrac{120\cdot119}{2}=60\cdot\dfrac{119}{2}⋮5\\ b,n^2+n+1=n\left(n+1\right)+1\)
Vì \(n\left(n+1\right)\) là tích 2 số tự nhiên lt nên \(n\left(n+1\right)\) chẵn
Do đó \(n\left(n+1\right)+1\) lẻ
Vậy \(n^2+n+1⋮̸4\)

\(B=2+2^2+2^3+...+2^{60}\)
\(=2\left(1+2+2^2\right)+...+2^{58}\left(1+2+2^2\right)\)
\(=7\cdot\left(2+...+2^{58}\right)⋮7\)

A = 11^9 + 11^8 + ... + 11 + 1
=> 11A = 11^10 + 11^9 +..........+ 11^2 + 11
11A - A = (11^10 + 11^9 +..........+ 11^2 + 11 ) - (11^9 + 11^8 + ... + 11 + 1)
10A = 11^10 - 1
A = (11^10 - 1 ) : 10
vì 11^10 có tận cùng = 1 => (11^10 - 1) có tận cùng = 0 =>(11^10 - 1 ) : 10 có tận cùng là 0 .
. Vậy A chia hết cho 5

sửa đề : CMR \(A=1^{19}+1^{18}+...+1^1+1\)
A = 1 + 1 + ... + 1 + 1 ( 20 số hạng )
A = 20 chia hết cho 5 => A chia hết cho 5 ( đpcm )

a) A > 1 20 + 1 20 + ... + 1 20 ⏟ 10 s o = 10 20 = 1 2 .
b) B = 1 5 + ... 1 9 + 1 10 + ... + 1 17 < 1 5 + ... + 1 5 ⏟ 5s o + 1 8 + ... + 1 8 ⏟ 8s o = 2
c) C = 1 10 + 1 11 + 1 12 ... + 1 18 + 1 19 < 1 10 + 1 10 + ... 1 10 ⏟ 9 s o = 1

A = 3 + 32 + 34 + 35 + 36 + ..... +3117 + 3118 + 3119 + 3120
3A = 32 + 34 + 35 + 36 + ..... +3117 + 3118 + 3119 + 3120 + 3121
3A - A = ( 32 + 34 + 35 + 36 + ..... +3117 + 3118 + 3119 + 3120 + 3121 ) - ( 3 + 32 + 34 + 35 + 36 + ..... +3117 + 3118 + 3119 + 3120 )
2A = 3121 - 3
A = ( 3121 - 3 ) : 2 chia hết cho 2
Vậy A chia hết cho 2
A = 3 +32+33+34+35+36+...+3117+3118+3119+3120
A = (3+32) + (33+34) + (35+36)+ ...+ (3177+3118) + (3119+3120)
A= 3 . (1+3) + 33(1+3 )+ 37 ( 1+3 ) +...+3117 ( 1+3 ) + 3119 ( 1+3 )
A=3. 4 + 33 . 4 + 35 . 4 + ...+ 3119 . 4
A =4. ( 3+33 + 35 + ... + 3119 ) ⋮ 2
( vì trong tích trên có thừa số 4 , mà trong tích nếu có bất kì số nào đó chia hết cho a thì tích đó chia hết cho a . Vậy tích trên có chữ số 4 vì vậy tích đó chia hết cho 2 )