Cho: S = 1 11 +...

Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mua vip

Pham Trong Bach

1 tháng 8 2017

Cho:

S = 1 11 + 1 12 + 1 13 + 1 14 + 1 15 + 1 16 + 1 17 + 1 18 + 1 19 + 1 20

Hãy so sánh S và 1 2

#Toán lớp 6

Cao Minh Tâm

1 tháng 8 2017

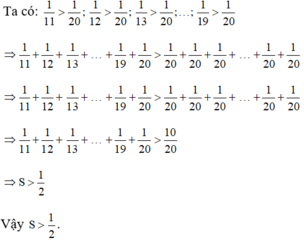
Giải sách bài tập Toán 6 | Giải bài tập Sách bài tập Toán 6

Đúng(0)

Các câu hỏi dưới đây có thể giống với câu hỏi trên

Sách Giáo Khoa

15 tháng 5 2017

Cho :

\(S=\dfrac{1}{11}+\dfrac{1}{12}+\dfrac{1}{13}+\dfrac{1}{14}+\dfrac{1}{15}+\dfrac{1}{16}+\dfrac{1}{17}+\dfrac{1}{18}+\dfrac{1}{19}+\dfrac{1}{20}\)

Hãy so sánh S và \(\dfrac{1}{2}\)

#Toán lớp 6

Giang Thủy Tiên

28 tháng 2 2018

Ta có :

\(\dfrac{1}{11}>\dfrac{1}{20}\\ \dfrac{1}{12}>\dfrac{1}{20}\\ ..........\\ \dfrac{1}{20}=\dfrac{1}{20}\)

\(\Rightarrow\dfrac{1}{11}+\dfrac{1}{12}+\dfrac{1}{13}+...+\dfrac{1}{20}>\dfrac{1}{20}+\dfrac{1}{20}+...+\dfrac{1}{20}\\ \Rightarrow S>\dfrac{10}{20}\\ \Rightarrow S>\dfrac{1}{2}\)

Đúng(0)

๖ۣۜHυү♜(♜๖ۣۜTεαм♜๖ۣۜTαм♜๖ۣۜGĭá¢♜๖ۣۜ...

27 tháng 2 2019 - olm

\(S=\frac{1}{11}+\frac{1}{12}+\frac{1}{13}+\frac{1}{14}+\frac{1}{15}+\frac{1}{16}+\frac{1}{17}+\frac{1}{18}+\frac{1}{19}+\frac{1}{20}\)

Hãy so sánh S và \(\frac{1}{2}\)

#Toán lớp 6

zZz Cool Kid_new zZz

27 tháng 2 2019

\(S=\frac{1}{11}+\frac{1}{12}+\frac{1}{13}+\frac{1}{14}+....+\frac{1}{20}\)

\(=\left(\frac{1}{11}+\frac{1}{12}+\frac{1}{13}+\frac{1}{14}+\frac{1}{15}\right)+\left(\frac{1}{16}+\frac{1}{17}+\frac{1}{18}+\frac{1}{19}+\frac{1}{20}\right)\)

\(>\frac{1}{15}\cdot5+\frac{1}{20}\cdot5\)

\(=\frac{1}{3}+\frac{1}{4}\)

\(=\frac{7}{12}>\frac{6}{12}=\frac{1}{2}\)

\(\Rightarrow S>\frac{1}{2}\)

Đúng(0)

✫¸.•°*”˜˜”*°•✫ Ṱђầภ Ḉђết ✫•°*”˜˜”*°...

27 tháng 2 2019

Bài làm

Ta có:

\(\frac{1}{11}>\frac{1}{20}\), \(\frac{1}{12}>\frac{1}{20}\), \(\frac{1}{13}>\frac{1}{20}\), \(\frac{1}{14}>\frac{1}{20}\), \(\frac{1}{15}>\frac{1}{20}\), \(\frac{1}{16}>\frac{1}{20}\), \(\frac{1}{17}>\frac{1}{20}\), \(\frac{1}{18}>\frac{1}{20}\),\(\frac{1}{19}>\frac{1}{20}\)

=> \(S=\frac{1}{11}+\frac{1}{12}+\frac{1}{13}+\frac{1}{14}+\frac{1}{15}+\frac{1}{16}+\frac{1}{17}+\frac{1}{18}+\frac{1}{19}+\frac{1}{20}>\frac{1}{20}\)

hay \(\frac{1}{20}+\frac{1}{20}+\frac{1}{20}+\frac{1}{20}+\frac{1}{20}+\frac{1}{20}+\frac{1}{20}+\frac{1}{20}+\frac{1}{20}+\frac{1}{20}\)

=> \(S=\frac{1}{20}.10=\frac{10}{20}=\frac{1}{2}\)

Do đó: \(S=\frac{1}{2}\)

# Chúc bạn học tốt #

Đúng(0)

Đông joker

7 tháng 3 2016 - olm

Cho S = \(\frac{1}{11}+\frac{1}{12}+\frac{1}{13}+\frac{1}{14}+\frac{1}{15}+\frac{1}{16}+\frac{1}{17}+\frac{1}{18}+\frac{1}{19}+\frac{1}{20}\)

Hãy so sánh S và \(\frac{1}{2}\)

#Toán lớp 6

Trần Hà Mi

8 tháng 3 2016 - olm

Cho \(S=\frac{1}{11}+\frac{1}{12}+\frac{1}{13}+\frac{1}{14}+\frac{1}{15}+\frac{1}{16}+\frac{1}{17}+\frac{1}{18}+\frac{1}{19}+\frac{1}{20}\)

Hãy so sánh S với \(\frac{1}{2}\)

#Toán lớp 6

Phạm Ngọc Anh

9 tháng 3 2017

Cho S= \(\frac{1}{11}+\frac{1}{12}+\frac{1}{13}+\frac{1}{14}+\frac{1}{15}+\frac{1}{16}+\frac{1}{17}+\frac{1}{18}+\frac{1}{19}+\frac{1}{20}\)

So sánh S với \(\frac{1}{2}\)

#Toán lớp 6

Đoàn Thị Lệ

12 tháng 3 2017

mình học toán cảm thấy nhức óc lắm, hoa mắt luôn

Đúng(0)

Khang khong manh

9 tháng 3 2017

Ta thấy:

1/11<1/4

1/12<1/4

.......

1/20<1/4

Suy ra ta có:

(1/11+1/12+1/13+1/14+1/15+1/16+1/17+1/18+1/19+1/20)<1/4 nhân 2 hay chính là nhỏ hơn 1/2

Đúng(0)

Hồ Hương Quế

14 tháng 3 2017 - olm

Cho S = \(\frac{1}{11}\)+ \(\frac{1}{12}\)+\(\frac{1}{13}\)+\(\frac{1}{14}\)+ \(\frac{1}{15}\)+\(\frac{1}{16}\)+\(\frac{1}{17}\)+\(\frac{1}{18}\)+\(\frac{1}{19}+\frac{1}{20}\)

Hãy so sánh S và \(\frac{1}{2}\)

#Toán lớp 6

SKTS_BFON

15 tháng 3 2017

Ta có:

\(\frac{1}{11}>\frac{1}{20}\)

\(\frac{1}{12}>\frac{1}{20}\)

\(...............\)

\(\frac{1}{19}>\frac{1}{20}\)

\(\frac{1}{20}=\frac{1}{20}\)

\(\Rightarrow\frac{1}{11}+\frac{1}{12}+......+\frac{1}{19}+\frac{1}{20}>\frac{10}{20}\) ( vì S có 20 số hạng )

\(\Rightarrow S>\frac{1}{2}\)

Vậy: \(S>\frac{1}{2}\)

Đúng(0)

Le Mai Phuong

13 tháng 3 2017

Cho S = \(\dfrac{1}{11}+\dfrac{1}{12}+\dfrac{1}{13}+\dfrac{1}{14}+\dfrac{1}{15}+\dfrac{1}{16}+\dfrac{1}{17}+\dfrac{1}{18}+\dfrac{1}{19}+\dfrac{1}{20}\). Hãy so sánh S và \(\dfrac{1}{2}\)

#Toán lớp 6

Trương Hồng Hạnh

13 tháng 3 2017

Ta có: \(\dfrac{1}{11}>\dfrac{1}{20}\)

\(\dfrac{1}{12}>\dfrac{1}{20}\)

\(\dfrac{1}{13}>\dfrac{1}{20}\)

\(\dfrac{1}{14}>\dfrac{1}{20}\)

\(\dfrac{1}{15}>\dfrac{1}{20}\)

\(\dfrac{1}{16}>\dfrac{1}{20}\)

\(\dfrac{1}{17}>\dfrac{1}{20}\)

\(\dfrac{1}{18}>\dfrac{1}{20}\)

\(\dfrac{1}{19}>\dfrac{1}{20}\)

\(\dfrac{1}{20}=\dfrac{1}{20}\)

=> \(\dfrac{1}{11}+\dfrac{1}{12}+...+\dfrac{1}{20}>\dfrac{1}{20}.10\)

hay S > \(\dfrac{1}{2}\)

Đúng(0)

Trần Quỳnh Mai

13 tháng 3 2017

Ta có :

\(\dfrac{1}{11}>\dfrac{1}{20}\) ( vì 1 > 0 , 0 < 11 < 20 )

\(\dfrac{1}{12}>\dfrac{1}{20}\) ( vì 1 > 0 , 0 < 12 < 20 )

...

\(\dfrac{1}{20}=\dfrac{1}{20}\)

\(\Rightarrow\dfrac{1}{11}+\dfrac{1}{12}+\dfrac{1}{13}+...+\dfrac{1}{20}>\dfrac{1}{20}+\dfrac{1}{20}+...+\dfrac{1}{20}\)( 10 số hạng )

\(\Rightarrow S>\dfrac{1}{20}.10\Rightarrow S>\dfrac{10}{20}\Rightarrow S>\dfrac{1}{2}\)

Vậy ...

Đúng(0)

nguyen van tu

9 tháng 3 2017 - olm

Cho S = 1/11+1/12+1/13+1/14+1/15+1/16+1/17+1/18+1/19+1/20. Hãy so sánh S và 1/2

#Toán lớp 6

Pokemon XYZ

9 tháng 3 2017

ta thấy: 1/11;1/12;1/13;...;1/19;1/20 đều >1/20

=>1/11+1/12+...1/19+1/20>1/20+1/20...+1/20

1/11+1/12+...1/19+1/20>10/20

1/11+1/12+...1/19+1/20>1/2 vậy S>1/2

Đúng(2)

Võ trần nam phương

28 tháng 2 2018 - olm

Cho S =1/11+1/12+1/13+1/14+1/15+1/16+1/17+1/18+1/19+1/20

Hãy so sánh S và 1/2

#Toán lớp 6

Vo Van Thuan Ky

28 tháng 2 2018

\(\frac{1}{11}\)> \(\frac{1}{20}\)

\(\frac{1}{12}\)> \(\frac{1}{20}\)

\(\frac{1}{19}\)>\(\frac{1}{20}\)

\(\frac{1}{20}\)= \(\frac{1}{20}\)

=> S = 1/11+1/12+...+1/20>1/20+1/20+1/20+1/20+1/20+1/20+1/20+1/20+1/20+1/20=10*1/20=1/2 (đpcm)

Đúng(0)

tth_new

28 tháng 2 2018

Ta có:

\(\frac{1}{11}>\frac{1}{20}\)

\(\frac{1}{12}>\frac{1}{20}\)

.............

\(\frac{1}{20}=\frac{1}{20}\)

\(\Rightarrow\frac{1}{11}+\frac{1}{12}+...+\frac{1}{20}>\frac{1}{20}+\frac{1}{20}+...+\frac{1}{20}\) ( 10 phân số \(\frac{1}{20}\))

\(\Leftrightarrow\frac{10.1}{20}=\frac{10}{20}=\frac{1}{2}\)

Vì \(\frac{1}{20}+\frac{1}{20}+...+\frac{1}{20}=\frac{1}{2}\). Mà \(\frac{1}{11}+\frac{1}{12}+...+\frac{1}{20}>\frac{1}{20}\Rightarrow\frac{1}{11}+\frac{1}{12}+...+\frac{1}{20}>\frac{1}{2}\)

Đúng(0)

nguyễn duy hưng

10 tháng 5 2018 - olm

Cho S=1/11+1/12+1/13+1/14+1/15+1/16+1/17+1/18+1/19+1/20.

Hãy so sánh S và 1/2

#Toán lớp 6

Arima Kousei

10 tháng 5 2018

Số lượng số của S là :

\(\left(20-11\right):1+1=10\)( số )

Ta có :
\(\frac{1}{11}>\frac{1}{20};\frac{1}{12}>\frac{1}{20};...;\frac{1}{19}>\frac{1}{20};\frac{1}{20}=\frac{1}{20}\)

\(\Rightarrow\frac{1}{11}+\frac{1}{12}+...+\frac{1}{20}>\frac{1}{20}+\frac{1}{20}+...+\frac{1}{20}\)

\(\Rightarrow S>\frac{1}{20}.10\)

\(\Rightarrow S>\frac{1}{2}\)

Vậy \(S>\frac{1}{2}\)

Đúng(0)

Nguyễn Hữu Đăng

10 tháng 5 2018

Ta có:

1/11 + 1/12 + 1/13 + ....................... + 1/ 20 > 1/20 +1/20 +1/ 20 +1/20 +1/20 +1/20 +1/20 +1/ 20 +1/20 +1/20 = 1/2

=> S > 1/2

Vậy S > 1/2

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP