Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

bn có thể lên trang học 24h mà kb với những người từ lp 6 trở lên rồi hỏi bài họ là đc mà!
tk nha!

Số tam giác có được là:
\(C^2_3\cdot C^1_4+C^1_3\cdot C^2_4=30\)
1 tam giác có 3 đỉnh ko thẳng hàng.
Theo NL Đi-rích-lê, có 3 điểm, 2 đường thẳng => Có 1 đường thẳng chứa 2 điểm, đường thẳng kia chứa điểm còn lại
Ta chia trường hợp:
*TH1: 2 điểm trên đường thẳng a, 1 điểm trên đường thẳng b
+) Điểm 1 trên a có 3 cách chọn
Điểm 2 trên a có 2 cách chọn
+) Điểm 1 trên b có 1 cách chọn
=> Tạo được 3.2.1 = 6 (tam giác)
*TH2: 1 điểm trên a, 2 điểm trên b
+) Điểm 1 trên a có 1 cách chọn
+) Điểm 1 trên b có 4 cách chọn
Điểm 2 trên b có 3 cách chọn
=> Tạo được 1.3.4 = 12 (tam giác)
Vậy tạo được tất cả 6+12=18 tam giác từ 7 điểm trên.

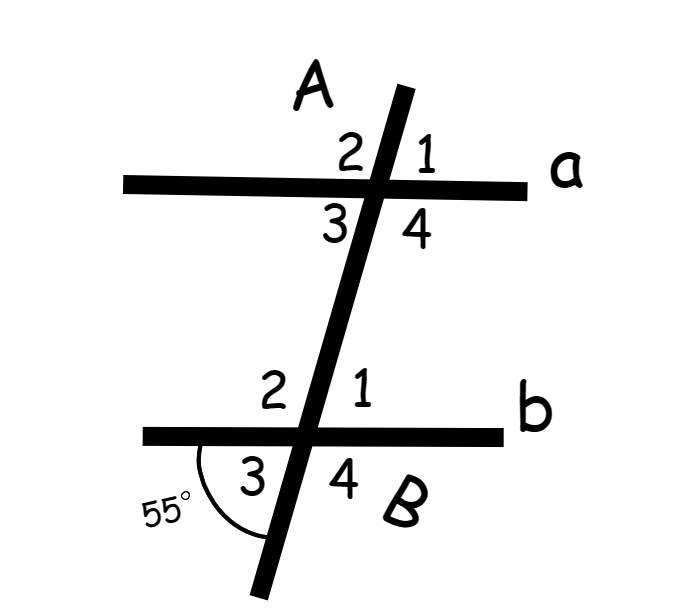
a) \(\widehat{B_1}=\widehat{B_3}=55^o\)
Hai góc đối đỉnh
Mà: \(\widehat{B_3}+\widehat{B_4}=180^o\) (kề bù)
\(\Rightarrow\widehat{B_4}=180^o-55^o=125^o\)
Mà: \(\widehat{B_2}=\widehat{B_4}=125^o\) (đối đỉnh)
b) Ta có: a//b
\(\Rightarrow\widehat{B_3}=\widehat{A_3}=55^o\)
Hai góc đồng vị
Mà: \(\widehat{B_2}=\widehat{A_4}=125^o\)
Hai góc so le trong
Mà: \(\widehat{B_1}=\widehat{A_1}=55^o\)
Đồng vị
Mà: \(\widehat{B_2}=\widehat{A_2}=125^o\)
Hai góc đồng vị