HL
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CB
1
H9
HT.Phong (9A5)
CTVHS
20 tháng 8 2023
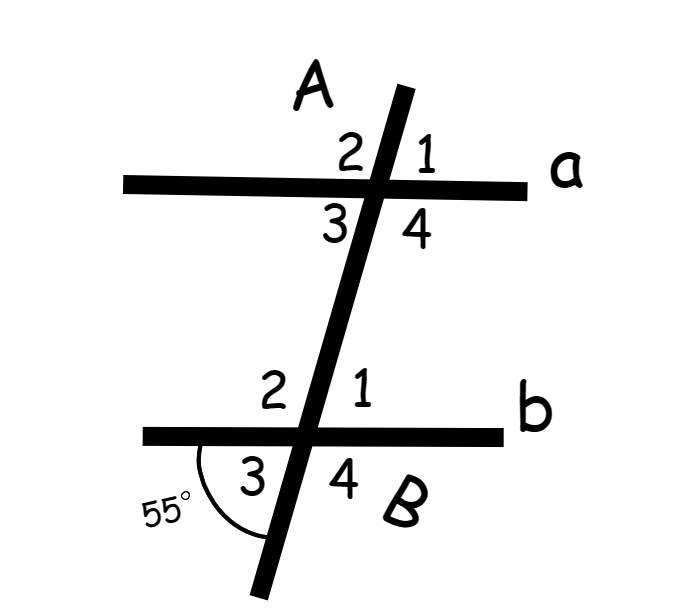
a) \(\widehat{B_1}=\widehat{B_3}=55^o\)
Hai góc đối đỉnh
Mà: \(\widehat{B_3}+\widehat{B_4}=180^o\) (kề bù)
\(\Rightarrow\widehat{B_4}=180^o-55^o=125^o\)
Mà: \(\widehat{B_2}=\widehat{B_4}=125^o\) (đối đỉnh)
b) Ta có: a//b
\(\Rightarrow\widehat{B_3}=\widehat{A_3}=55^o\)
Hai góc đồng vị
Mà: \(\widehat{B_2}=\widehat{A_4}=125^o\)
Hai góc so le trong
Mà: \(\widehat{B_1}=\widehat{A_1}=55^o\)
Đồng vị
Mà: \(\widehat{B_2}=\widehat{A_2}=125^o\)
Hai góc đồng vị
31 tháng 3 2023
|
Xét tổng
Suy ra có ít nhất một trong 7 số |
là số chẵn
27 tháng 12 2015
giả sử P lẻ thì a1-b2;a2-b2;a2003-b2003 lẻ.khi đó, (a1-b1)+(a2-b2)+...+(a2003-b2003) lẻ(vì có 2003 cặp số lẻ) (1)
mà (a1-b1)+(a2-b2)+...+(a2003-b2003)=(a1+a2+...+a2003)-(b1+b2+...+b2003). vì b1;b2;b3;...;b2003 là cách sắp xếp theo thứ tự khác của a1;a2;a3;...;a2003 nên (a1+a2+...+a2003)-(b1+b2+...+b2003)=0(2)
do (1) và(2) mâu thuẫn nên P ko thể là số lẻ, vậy P là số chẵn(đpcm)
tick
nha
8 tháng 4 2023
Số tam giác có được là:
\(C^2_3\cdot C^1_4+C^1_3\cdot C^2_4=30\)
VD
8 tháng 4 2023
1 tam giác có 3 đỉnh ko thẳng hàng.
Theo NL Đi-rích-lê, có 3 điểm, 2 đường thẳng => Có 1 đường thẳng chứa 2 điểm, đường thẳng kia chứa điểm còn lại
Ta chia trường hợp:
*TH1: 2 điểm trên đường thẳng a, 1 điểm trên đường thẳng b
+) Điểm 1 trên a có 3 cách chọn
Điểm 2 trên a có 2 cách chọn
+) Điểm 1 trên b có 1 cách chọn
=> Tạo được 3.2.1 = 6 (tam giác)
*TH2: 1 điểm trên a, 2 điểm trên b
+) Điểm 1 trên a có 1 cách chọn
+) Điểm 1 trên b có 4 cách chọn
Điểm 2 trên b có 3 cách chọn
=> Tạo được 1.3.4 = 12 (tam giác)
Vậy tạo được tất cả 6+12=18 tam giác từ 7 điểm trên.