Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tính số đường thẳng: Gọi X là tập hợp các điểm đã cho, S là tập hợp các điểm thẳng hàng và \(T=X\backslash S\). Qua 5 điểm thuộc S, ta vẽ được duy nhất 1 đường thẳng. Xét 1 điểm bất kì trong S, nó kết nối với 15 điểm không thuộc S bằng 1 đường thẳng. Tương tự với các điểm còn lại trong S, số đường thẳng nối từ các điểm thuộc S đến các điểm còn lại là \(5.15=75\) đường. Xét các điểm thuộc T, do trong các điểm thuộc T không có 3 điểm nào thẳng hàng nên số đường thẳng kết nối 15 điểm này là \(C^2_{15}\). Vậy có tất cả \(1+75+C^2_{15}=181\) đường thẳng từ 20 điểm đã cho.
Tính số tam giác: Xét 2 điểm bất kì thuộc S, có 15 tam giác được tạo thành từ 2 điểm đó và 1 điểm thuộc T. Số cách chọn 2 điểm thuộc S là \(C^2_5\), do đó số tam giác tạo thành bằng cách chọn 2 điểm thuộc S và 1 điểm thuộc T là \(C^2_5.15\). Xét 3 điểm bất kì thuộc T, có tất cả \(C^3_{15}\) tam giác. Vậy có tất cả \(C^2_5.15+C^3_{15}=605\) tam giác được tạo thành từ 20 điểm đã cho.

Cách 1:
TH1: 2 điểm thuộc a và 1 điểm thuộc b
Số cách chọn 2 điểm thuộc đường thẳng a là \(C_3^2\) (cách chọn)
Số cách chọn 1 điểm thuộc đường thẳng b là: \(C_4^1\) (cách chọn)
=> Số tam giác tạo thành là: \(C_3^2 . C_4^1 = 12\)
TH2: 2 điểm thuộc b và 1 điểm thuộc a
Số cách chọn 2 điểm thuộc đường thẳng b là \(C_4^2\) (cách chọn)
Số cách chọn 1 điểm thuộc đường thẳng a là: \(C_3^1\) (cách chọn)
=> Số tam giác tạo thành là: \(C_4^2 + C_3^1 = 18\)
Vậy có tất cả 12 + 18 = 30 tam giác.
Cách 2:
Số cách chọn 3 điểm thuộc đường thẳng a là: \(C_3^3\) (cách chọn)
Số cách chọn 3 điểm thuộc đường thẳng b là: \(C_4^3\) (cách chọn)
Số cách chọn 3 điểm bất kì trong 7 điểm đã cho là: \(C_7^3\) (cách chọn)
Số cách chọn 3 điểm không thẳng hàng trong 7 điểm đã cho là: \(C_7^3 - C_4^3 - C_3^3 = 30\) (cách chọn)
Vậy số tam giác có thể có là : 30 (tam giác)

a: Số tam giác tạo được là;
\(C^2_{12}\cdot3+C^3_{12}=418\)
b: Số tam giác tạo thành là:
\(C^2_9\cdot6+C^3_9=300\)

Cách 1:
TH 1: Chọn 2 điểm thuộc đường thẳng có 4 điểm
Chọn 2 điểm từ đường thẳng trên có \(C_4^2\) cách
Chọn 1 điểm từ đường thẳng còn lại có 5 cách
=> Số tam giác tạo thành là \(5.C_4^2 = 30\)
TH 2: Chọn 2 điểm thuộc đường thẳng có 5 điểm
Chọn 2 điểm từ đường thẳng dưới có \(C_5^2\) cách
Chọn 1 điểm từ đường thẳng còn lại có 4 cách
=> Số tam giác tạo thành là \(4.C_5^2 = 40\)
Vậy có tất cả 70 tam giác được tạo thành.
Cách 2:
Số cách chọn 3 điểm bất kì là: \(C_9^3 = 84\) cách
Số cách chọn 3 điểm thẳng hàng là: \(C_4^3 +C_5^3 =14 \) cách
=> Số cách chọn 3 điểm không thẳng hàng là: 84 - 14 = 70 (cách)
Do đó ta có thể có 70 tam giác.

Tham khảo:
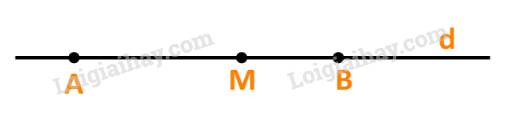
a) Điểm M thuộc đường thẳng d khi và chỉ khi hai vecto \(\overrightarrow {AM} \) và \(\overrightarrow {AB} \) cùng phương (cùng giá d)
Khi và chỉ khi tồn tại số t để \(\overrightarrow {AM} = t.\overrightarrow {AB} \).
Vậy khẳng định a) đúng.
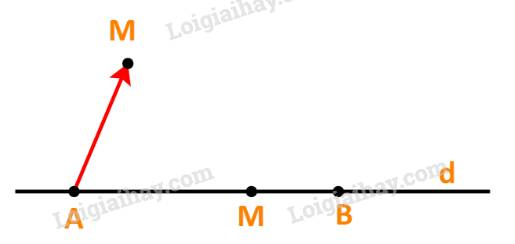
b) Với điểm M bất kì, ta luôn có \(\overrightarrow {AM} = \frac{{AM}}{{AB}}.\overrightarrow {AB} \)
Sai vì \(\overrightarrow {AM} = \frac{{AM}}{{AB}}.\overrightarrow {AB} \) khi và chỉ khi \(\overrightarrow {AM} \) và \(\overrightarrow {AB} \) cùng hướng.
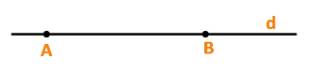
c) Điểm M thuộc tia đối của tia AB, tức là A nằm giữa M và B.
Khi và chỉ khi hai vecto \(\overrightarrow {AM} \) và \(\overrightarrow {AB} \) ngược hướng
\( \Leftrightarrow \) tồn tại số \(t \le 0\) để \(\overrightarrow {AM} = t.\overrightarrow {AB} \)
Vậy khẳng định c) đúng.


Đáp án: B
a, b đúng.
c sai vì Góc tạo bởi hai tia phân giác của hai góc kề bù là góc vuông không phải góc nhọn.
d sai vì Trong các đường xiên và đường vuông góc kẻ từ một điểm ở ngoài một đường thẳng đến dường thẳng đó, đường vuông góc là đường ngắn nhất không phải dài nhất.

a.
\(\overrightarrow{AB}=\left(3;-4\right)\Rightarrow\) đường thẳng AB nhận (4;3) là 1 vtpt
Phương trình AB:
\(4\left(x-2\right)+3\left(y-5\right)=0\Leftrightarrow4x+3y-23=0\)b.
Do d vuông góc delta nên d nhận (4;-3) là 1 vtpt
Phương trình d có dạng: \(4x-3y+c=0\)
\(d\left(B;d\right)=\dfrac{\left|4.5-3.1+c\right|}{\sqrt{4^2+\left(-3\right)^2}}=\dfrac{1}{5}\)
\(\Rightarrow\left|c+17\right|=1\Rightarrow\left[{}\begin{matrix}c=-16\\c=-18\end{matrix}\right.\)
Có 2 đường thẳng d thỏa mãn: \(\left[{}\begin{matrix}4x-3y-16=0\\4x-3y-18=0\end{matrix}\right.\)
Giải:
Gọi số điểm là n.
Ta có công thứ tổng quát tính số đường thẳng là:
\(\dfrac{n\left(n-1\right)}{2}\)
Thay vào, ta được:
\(\dfrac{100\left(100-1\right)}{2}=\dfrac{100.99}{2}=4950\)
Vậy ...
Chúc bạn học tốt!