Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Một đoạn thẳng được tạo bởi 2 điểm bất kì
Nên để có một đoạn thẳng có điểm mút thuộc các điểm đã cho thì ta chọn 2 điểm bất kì từ 6 điểm đã cho, mỗi cách chọn 2 điểm từ 6 điểm đã cho là một tổ hợp chập 2 của 6, từ đó số đoạn thẳng có điểm đầu mút thuộc các điểm đã cho được tạo ra là:
\(C_6^2 = \frac{{6!}}{{2!.4!}} = 15\) (đoạn thẳng)
b) Mỗi tam giác được tạo bởi 3 điểm không thẳng hàng, nên để có một tam giác mà các đỉnh của nó là các điểm đã cho thì ta chọn 3 điểm bất kì từ 6 điểm đã cho, mỗi cách chọn 3 điểm từ 6 điểm là một tổ hợp chập 3 của 6, từ đó số tam giác có đỉnh thuộc các điểm đã cho là:
\(C_6^3 = \frac{{6!}}{{3!.3!}} = 20\) (tam giác)

Cách 1:
TH1: 2 điểm thuộc a và 1 điểm thuộc b
Số cách chọn 2 điểm thuộc đường thẳng a là \(C_3^2\) (cách chọn)
Số cách chọn 1 điểm thuộc đường thẳng b là: \(C_4^1\) (cách chọn)
=> Số tam giác tạo thành là: \(C_3^2 . C_4^1 = 12\)
TH2: 2 điểm thuộc b và 1 điểm thuộc a
Số cách chọn 2 điểm thuộc đường thẳng b là \(C_4^2\) (cách chọn)
Số cách chọn 1 điểm thuộc đường thẳng a là: \(C_3^1\) (cách chọn)
=> Số tam giác tạo thành là: \(C_4^2 + C_3^1 = 18\)
Vậy có tất cả 12 + 18 = 30 tam giác.
Cách 2:
Số cách chọn 3 điểm thuộc đường thẳng a là: \(C_3^3\) (cách chọn)
Số cách chọn 3 điểm thuộc đường thẳng b là: \(C_4^3\) (cách chọn)
Số cách chọn 3 điểm bất kì trong 7 điểm đã cho là: \(C_7^3\) (cách chọn)
Số cách chọn 3 điểm không thẳng hàng trong 7 điểm đã cho là: \(C_7^3 - C_4^3 - C_3^3 = 30\) (cách chọn)
Vậy số tam giác có thể có là : 30 (tam giác)

Số tam giác với 3 đỉnh là 3 điểm trong 8 điểm đã cho là tổ hợp chập 3 của 8 phần tử, do đó số tam giác là: \(C_8^3\) ( tam giác)

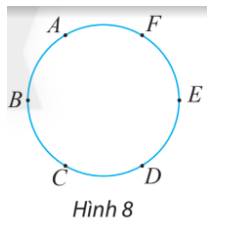
1). Tam giác ABF và tam giác ACE ần lượt cân tại F, E và
F B A ^ = E C A ^ = A ^ 2 ⇒ Δ A B F ∽ Δ A C E .
2). Giả sử G là giao điểm của BE và CF.
Ta có G F G C = B F C E = A B A C = D B D C ⇒ G D ∥ F B , và F B ∥ A D ta có G ∈ A D .
3). Chứng minh B Q G ^ = Q G A ^ = G A E ^ = G A C ^ + C A E ^ = G A B ^ + B A F ^ = G A F ^ , nên AGQF nội tiếp, và Q P G ^ = G C E ^ = G F Q ^ , suy ra tứ giác FQGP nội tiếp.
1) Chứng minh rằng tam giác \( A B F \) đồng dạng với tam giác \( A C E \):
- Tam giác \(ABF\) và \(ACE\) có:
+ Góc \(A\) chung.
+ Góc \(BAF\) bằng góc \(CAE\) (vì \(AD\) là phân giác của góc \(BAC\) và \(CF\), \(BE\) song song với \(AD\)).
Do đó, tam giác \(ABF\) đồng dạng với tam giác \(ACE\) (theo trường hợp góc-góc).
2) Chứng minh rằng các đường thẳng \(BE\), \(CF\), \(AD\) đồng quy:
- Gọi \(G\) là giao điểm của \(BE\) và \(CF\).
- \(AD\) là phân giác góc \(BAC\), và \(BE\), \(CF\) song song với \(AD\). Do đó, \(G\) cũng nằm trên phân giác \(AD\).
- Vậy \(BE\), \(CF\), \(AD\) đồng quy tại \(G\).
3) Chứng minh rằng các điểm \(A\), \(P\), \(G\), \(Q\), \(F\) cùng thuộc một đường tròn:
- Gọi đường tròn ngoại tiếp tam giác \(GEC\) là \(\omega\).
- \(QE\) cắt \(\omega\) tại \(P\) khác \(E\), vậy \(P\) nằm trên đường tròn \(\omega\).
- \(GQ\) song song với \(AE\), và \(AE\) là đường kính của \(\omega\) (vì \(E\) là trung điểm của \(AC\) và \(G\) nằm trên phân giác của \(BAC\)). Do đó, \(GQ\) là dây cung của \(\omega\).
- \(PF\) là tiếp tuyến của \(\omega\) tại \(P\) (vì \(QE\) là tiếp tuyến và \(PF\) là phần kéo dài của \(QE\)).
- Góc \(PGF\) bằng góc \(GAC\) (cùng chắn cung \(GC\) của \(\omega\)).
- \(AF\) là trung trực của \(AB\), nên \(ABF\) là tam giác cân tại \(A\). Do đó, góc \(AFB\) bằng góc \(ABF\).
- Góc \(ABF\) bằng góc \(GAC\) (do đồng dạng của tam giác \(ABF\) và \(ACE\)).
- Vậy, góc \(PGF\) bằng góc \(AFB\). Do đó, \(A\), \(P\), \(G\), \(Q\), \(F\) cùng thuộc một đường tròn.

AC vuông góc BH nên nhận (1;-1) là 1 vtpt
Phương trình AC:
\(1\left(x-1\right)-1\left(y-1\right)=0\Leftrightarrow x-y=0\)
A thuộc AC và d nên tọa độ A là nghiệm:
\(\left\{{}\begin{matrix}x-y=0\\x-4y-2=0\end{matrix}\right.\) \(\Rightarrow A\left(-\dfrac{2}{3};-\dfrac{2}{3}\right)\)
M là trung điểm AC \(\Rightarrow\left\{{}\begin{matrix}x_C=2x_M-x_A=\dfrac{8}{3}\\y_C=2y_M-y_A=\dfrac{8}{3}\end{matrix}\right.\) \(\Rightarrow C\left(\dfrac{8}{3};\dfrac{8}{3}\right)\)
BC song song d nên nhận (1;-4) là 1 vtpt
Phương trình BC:
\(1\left(x-\dfrac{8}{3}\right)-4\left(y-\dfrac{8}{3}\right)=0\Leftrightarrow x-4y+8=0\)
B là giao điểm của BC và BH nên tọa độ thỏa mãn:
\(\left\{{}\begin{matrix}x-4y+8=0\\x+y+3=0\end{matrix}\right.\) \(\Rightarrow B\left(-4;1\right)\)
\(\Rightarrow\overrightarrow{AB}=...\Rightarrow\) phương trình đường thẳng AB

Bạn xem lại đề ạ!
Nếu bạn đã chứng minh được D là trung điểm IQ; E là trung điểm KP; E là trung điểm KP; F là trung điểm LJ
Thì dễ dàng suy ra được: \(\overrightarrow{MD}=\frac{\overrightarrow{MI}+\overrightarrow{MQ}}{2}\); \(\overrightarrow{ME}=\frac{\overrightarrow{MK}+\overrightarrow{MP}}{2}\); \(\overrightarrow{MF}=\frac{\overrightarrow{MJ}+\overrightarrow{ML}}{2}\)
( Vì chúng ta có tính chất: Nếu I là trung điểm đoạn thẳng AB thì mọi điểm M ta có: \(2\overrightarrow{MI}=\overrightarrow{MA}+\overrightarrow{MB}\))
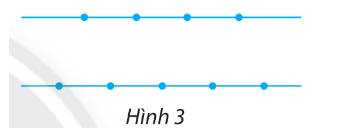
Cách 1:
TH 1: Chọn 2 điểm thuộc đường thẳng có 4 điểm
Chọn 2 điểm từ đường thẳng trên có \(C_4^2\) cách
Chọn 1 điểm từ đường thẳng còn lại có 5 cách
=> Số tam giác tạo thành là \(5.C_4^2 = 30\)
TH 2: Chọn 2 điểm thuộc đường thẳng có 5 điểm
Chọn 2 điểm từ đường thẳng dưới có \(C_5^2\) cách
Chọn 1 điểm từ đường thẳng còn lại có 4 cách
=> Số tam giác tạo thành là \(4.C_5^2 = 40\)
Vậy có tất cả 70 tam giác được tạo thành.
Cách 2:
Số cách chọn 3 điểm bất kì là: \(C_9^3 = 84\) cách
Số cách chọn 3 điểm thẳng hàng là: \(C_4^3 +C_5^3 =14 \) cách
=> Số cách chọn 3 điểm không thẳng hàng là: 84 - 14 = 70 (cách)
Do đó ta có thể có 70 tam giác.