
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


GỌI I LÀ GIAO ĐIỂM CỦA OE VÀ AC
D) XÉT \(\Delta COI\)VÀ\(\Delta AOI\)CÓ
\(CO=AO\left(GT\right)\)
\(\widehat{COE}=\widehat{IOA}\left(GT\right)\)
\(OI\)LÀ CẠNH CHUNG
\(\Rightarrow\Delta COI=\Delta AOI\left(C-G-C\right)\)
\(\Rightarrow\widehat{CIO}=\widehat{AIO}\)HAI GÓC TƯƠNG ỨNG
MÀ\(\widehat{OIC}+\widehat{OIA}=180^o\left(KB\right)\)
THAY\(\widehat{OIC}+\widehat{OIC}=180^o\)
\(2\widehat{OIC}=180^o\)
\(\widehat{OIC}=180^o:2=90^o\)
nên\(AC\perp OE\)TẠI I
E) CHỨNG MINH TƯƠNG TỰ CÂU D SAU ĐÓ => SO LE TRONG BẰNG NHAU=> //
E) GỌI M LÀ GIAO ĐIỂM CỦA OE VÀDB
VÌ OE LÀ PHÂN GIÁC CỦA GÓC O MÀ OE CŨNG THUỘC GÓC DEB
=> OE CŨNG LÀ TIA PHÂN GIÁC CỦA DEB
XÉT \(\Delta DEM\)VÀ \(\Delta MEB\)CÓ
\(DE=EB\left(\Delta EAB=\Delta ECD\right)\)
\(\widehat{DEM}=\widehat{MEB}\left(CMT\right)\)
EM LÀ CẠNH CHUNG
\(\Rightarrow\Delta DEM=\Delta MEB\left(C-G-C\right)\)
\(\Rightarrow\widehat{DME}=\widehat{EMB}\left(HCTU\right)\)
MÀ\(\widehat{DME}+\widehat{EMB}=180^o\left(kb\right)\)
THAY\(\widehat{DME}+\widehat{DME}=180^o\)
\(2\widehat{DME}=180^o\)
\(\widehat{DME}=180^o:2=90^O\)
\(\Rightarrow\widehat{OIA}=\widehat{DME}=90^O\)
HAI GÓC NÀY Ở VỊ TRÍ ĐỒNG VỊ BẰNG NHAU
\(\Rightarrow AC//BD\)

d: Xét ΔABC có
BK,CH là đường cao
BK cắt CH tại I
=>I là trực tâm
=>AI vuông góc BC
mà HF vuông góc BC
nên AI//HF
e: Xét ΔABC cân tại A có góc BAC=60 độ
nên ΔABC đều
Xét ΔABC đều có I là trực tâm
nên I là tâm đường tròn ngoại tiếp ΔABC
=>IA=IB=IC

a) Các vị trí so le trong, và đồng vị với \(\widehat{mAB}\) là:
\(\widehat{B_1};\widehat{APQ};\widehat{nPA}\)
b) Ta có: \(\widehat{B_1}=\widehat{mAB}=50^o\) (hai góc so le trong)
Mà: \(\widehat{B_1}+\widehat{B_2}=180^o\Rightarrow\widehat{B_2}=180^o-50^o=130^o\)
c) Ta có: \(\widehat{mAB}+\widehat{A_1}=180^o\Rightarrow\widehat{A_1}=180^o-\widehat{mAB}=180^o-50^o=130^o\)
Mà: \(\widehat{mAB}=\widehat{A_2}=50^o\)(hai góc đối đỉnh)
d) Ta có:
\(\widehat{APQ}+\widehat{PQB}=180^o\)
\(\Rightarrow\widehat{PQB}=180^o-\widehat{APQ}=180^o-110^o=70^o\)

a: AC=12cm
b: Xét ΔABE vuông tại A và ΔDBE vuông tại D có
BE chung
BA=BD
Do đó: ΔABE=ΔDBE
c: Xét ΔAEK vuông tại A và ΔDEC vuông tại D có
EA=ED
\(\widehat{AEK}=\widehat{DEC}\)
Do đó: ΔAEK=ΔDEC
Suy ra:EK=EC
suy ra tam giác vuông cần thêm vuông theo định lí nào chứ bạn?

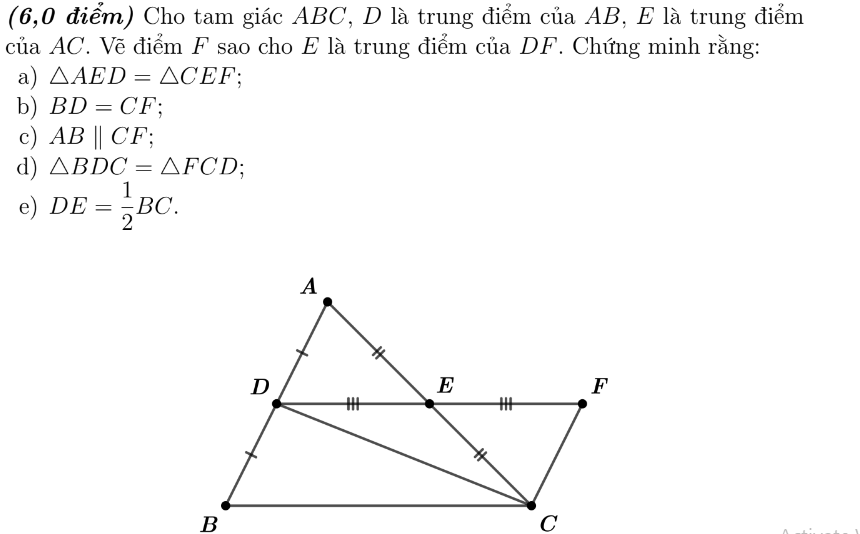
e: Xét ΔABC có
D là trung điểm của AB
E là trung điểm của AC
Do đó: DE là đường trung bình của ΔABC
Suy ra: \(DE=\dfrac{BC}{2}\)

a: P(x)=3x^4+6x^2-5x-2
Q(x)=-2x^6+2x^4+4x^2-5x-4
b: H(x)=P(x)-Q(x)
=3x^4+6x^2-5x-2+2x^6-2x^4-4x^2+5x+4
=2x^6+x^4+2x^2+2
c: H(x)=x^2(2x^4+x^2+2)+2>=2>0 với mọi x
=>H(x) ko có nghiệm


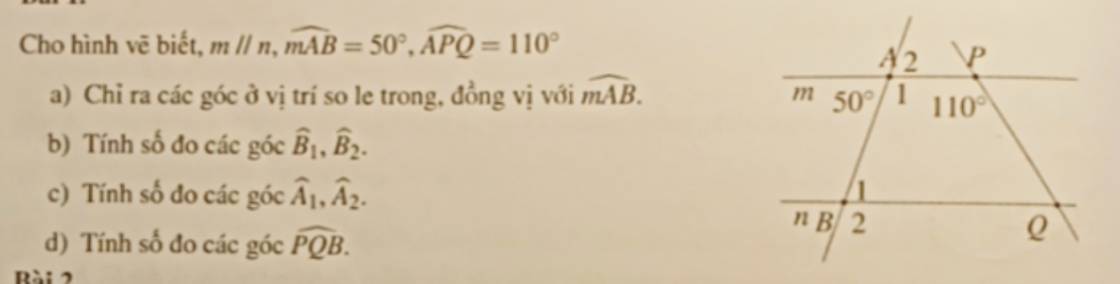
 AI CHỈ MÌNH CÂU E THÔI VỚI :(((
AI CHỈ MÌNH CÂU E THÔI VỚI :(((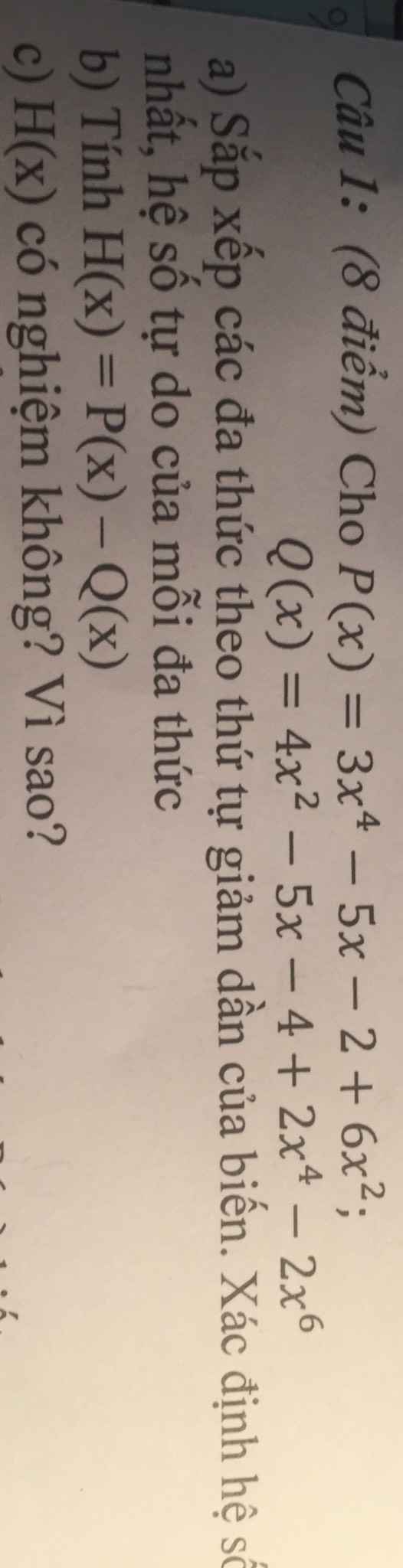

c)\(0,625+\left(\dfrac{-2}{7}\right)+\dfrac{3}{8}+\left(-\dfrac{5}{7}\right)+1\dfrac{2}{3}\)
\(=\dfrac{5}{8}-\dfrac{2}{7}+\dfrac{3}{8}-\dfrac{5}{7}+\dfrac{5}{3}\)
\(=\left(\dfrac{5}{8}+\dfrac{3}{8}\right)-\left(\dfrac{2}{7}+\dfrac{5}{7}\right)+\dfrac{5}{3}\)
\(=1-1+\dfrac{5}{3}\)
\(=\dfrac{5}{3}\)
d)\(\left(-3\right).\left(\dfrac{-38}{21}\right).\left(\dfrac{-7}{6}\right).\left(\dfrac{-3}{19}\right)\)
\(=\dfrac{\left(-3\right).\left(-38\right).\left(-7\right).\left(-3\right)}{21.6.19}\)
\(=\dfrac{\left(-3\right).\left(-2\right).19.\left(-7\right).\left(-3\right)}{3.7.3.2.19}\)
\(=1\)
e)\(\left(\dfrac{11}{18}:\dfrac{22}{9}\right).\dfrac{8}{5}\)
\(=\left(\dfrac{11}{18}.\dfrac{9}{22}\right).\dfrac{8}{5}\)
\(=\dfrac{11.9}{18.22}.\dfrac{8}{5}\)
\(=\dfrac{11.9.2.2.2}{2.9.11.2.5}\)(có thể bỏ qua bước này)
\(=\dfrac{2}{5}\)
g)\(\left[\left(-\dfrac{4}{5}\right).\dfrac{5}{8}\right]:\left(-\dfrac{25}{12}\right)\)
\(=\left[\dfrac{\left(-4\right).5}{5.8}\right].\dfrac{-12}{25}\)
\(=\dfrac{-1}{2}.\dfrac{-12}{25}\)
\(=\dfrac{6}{25}\)