Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

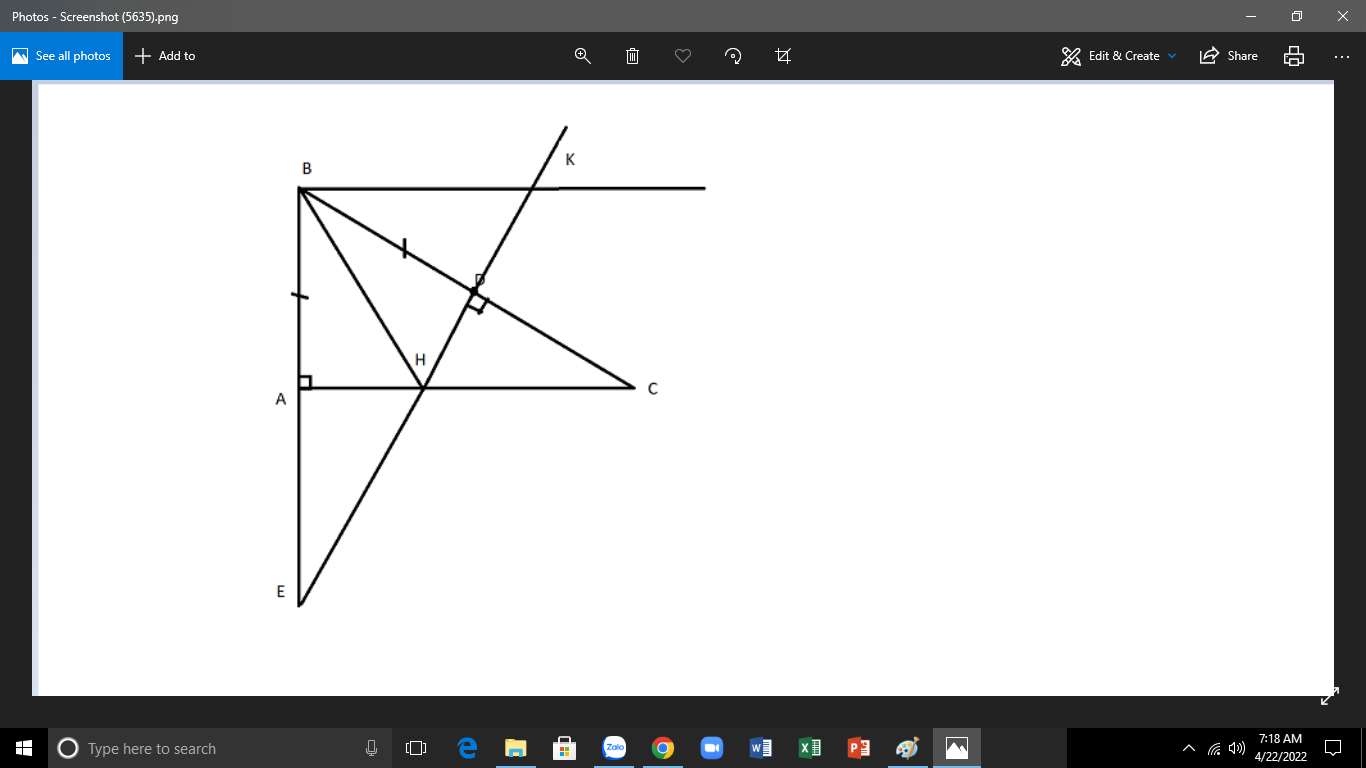
\(\text{a)Xét }\Delta ABC\text{ có:}\)
\(\widehat{A}+\widehat{B}+\widehat{C}=180^0\left(\text{tính chất tổng ba góc một tam giác}\right)\)
\(\Rightarrow\widehat{C}=180^0-\left(\widehat{A}+\widehat{B}\right)\)
\(\Rightarrow\widehat{C}=180^0-\left(90^0+60^0\right)=30^0\)
\(\text{Xét }\Delta ABC\text{ có:}\)
\(\widehat{A}>\widehat{B}>\widehat{C}\left(90^0>60^0>30^0\right)\)
\(\Rightarrow BC>AC>AB\left(\text{quan hệ giữa góc và cạnh đối diện trong tam giác}\right)\)
\(\Rightarrow AB< AC\)
\(b)\text{Xét }\Delta ABC\text{ và }\Delta DBE\text{ có:}\)
\(\left\{{}\begin{matrix}\widehat{B}\text{ chung}\\\widehat{BAC}=\widehat{BDE}=90^0\left(gt\right)\\BD=AB\left(gt\right)\end{matrix}\right.\)
\(\Rightarrow\Delta ABC=\Delta DBE\left(g-c-g\right)\)
\(c)\text{Xét }\Delta ABH\text{ và }\Delta DBH\text{ có:}\)
\(\left\{{}\begin{matrix}BD=AB\left(gt\right)\\BH\text{ chung}\\\widehat{BAH}=\widehat{BDH}=90^0\left(gt\right)\end{matrix}\right.\)
\(\Rightarrow\Delta ABH=\Delta DBH\left(ch-gn\right)\)
\(\Rightarrow\widehat{ABH}=\widehat{DBH}\left(\text{hai góc tương ứng}\right)\)
\(\Rightarrow BH\text{ là phân giác }\widehat{ABC}\)
\(d)\text{Mik k bt:< }\)

a: AC=4cm
b: Xét ΔBAE vuông tại A và ΔBDE vuông tại D có
BE chung
BA=BD
Do đó: ΔBAE=ΔBDE
Suy ra: \(\widehat{ABE}=\widehat{DBE}\)
hay BE là tia phân giác của góc ABC
c: Ta có: ΔBAE=ΔBDE
nên EA=ED
mà ED<EC
nên EA<EC
d: Ta có: BA=BD
nên B nằm trên đường trung trực của AD(1)
Ta có: EA=ED
nên E nằm trên đường trung trực của AD(2)
Từ (1) và (2) suy ra BE là đường trung trực của AD

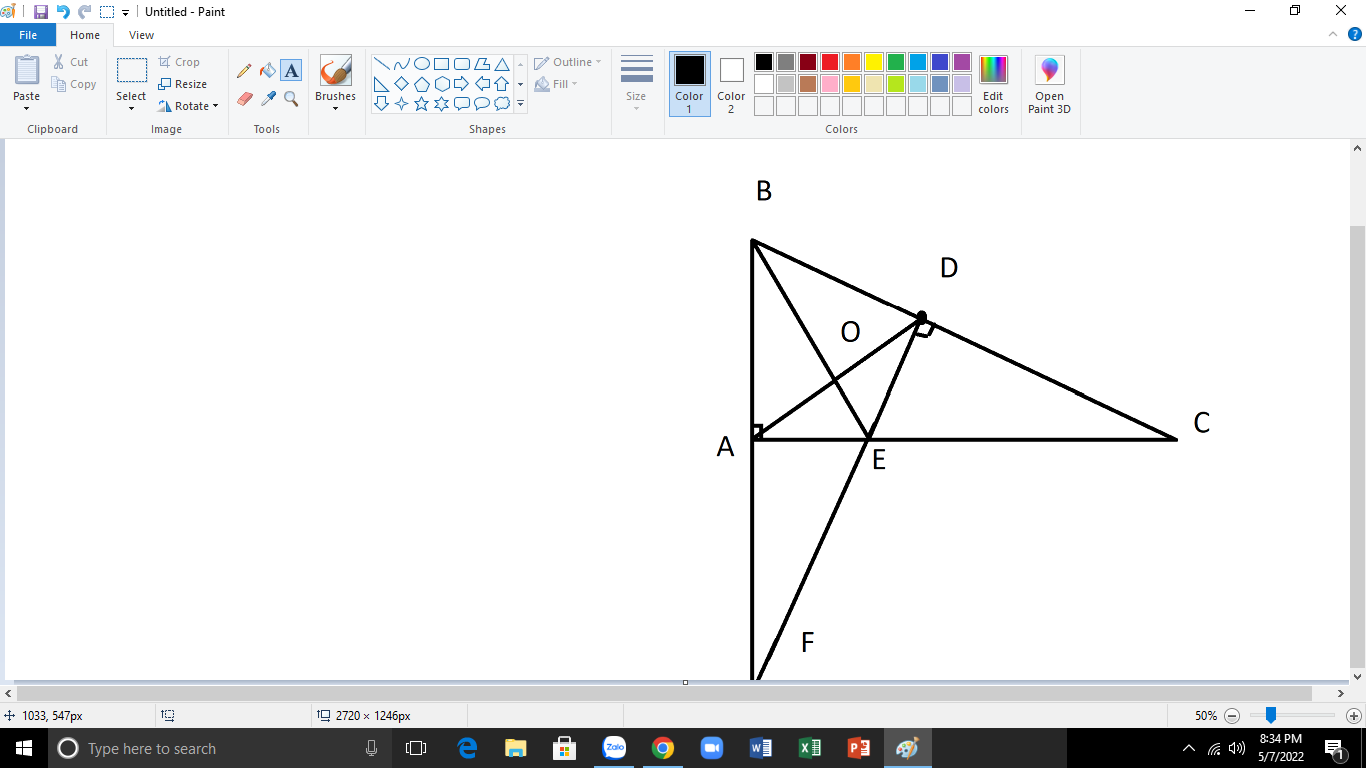
\(\text{a)Xét }\Delta ABC\text{ vuông tại A có:}\)
\(BC^2=AB+AC^2\left(\text{định lí Py ta go}\right)\)
\(\Rightarrow BC^2=5^2+7^2=25+49=74\left(cm\right)\)
\(\Rightarrow BC=\sqrt{74}\left(cm\right)\)
\(\text{b)Xét }\Delta ABE\text{ và }\Delta DBE\text{ có:}\)
\(\widehat{BAE}=\widehat{BDE}=90^0\left(gt\right)\)
\(BE\text{ chung}\)
\(BA=BD\left(gt\right)\)
\(\Rightarrow\Delta ABE=\Delta DBE\left(c-g-c\right)\)
\(\text{c)Xét }\Delta AEF\text{ và }\Delta DEC\text{ có:}\)
\(\widehat{AEF}=\widehat{DEC}\left(\text{đối đỉnh}\right)\)
\(\widehat{FAE}=\widehat{CDE}=90^0\left(gt\right)\)
\(AE=DE\left(\Delta ABE=\Delta DBE\right)\)
\(\Rightarrow\Delta AEF=\Delta DEC\left(g-c-g\right)\)
\(\Rightarrow EF=EC\left(\text{hai cạnh tương ứng}\right)\)
\(\text{d)Gọi O là giao điểm của BE và AD}\)
\(\text{Xét }\Delta ABO\text{ và }\Delta DBO\text{ có:}\)
\(BO\text{ chung}\)
\(BA=BD\left(gt\right)\)
\(\widehat{ABO}=\widehat{DBO}\left(\Delta ABE=\Delta DBE\right)\)
\(\Rightarrow\Delta ABO=\Delta DBO\left(c-g-c\right)\)
\(\Rightarrow\widehat{AOB}=\widehat{DOB}\left(\text{hai góc tương ứng}\right)\)
\(\text{Mà chúng kề bù}\)
\(\Rightarrow\widehat{AOB}=\widehat{DOB}=\dfrac{180^0}{2}=90^0\)
\(\Rightarrow BE\perp AD\)
\(\text{Mà AO=DO}\left(\Delta AOB=\Delta DOB\right)\)
\(\Rightarrow BE\text{ là đường trung trực của đoạn thẳng AD}\)
cảm ơn bạn nghe thank you mà làm thế này đúng ko bạn:
a) Vì tam giác BAC vuông tại A
=> AB^2 + AC^2 = BC^2 ( đl pytago )
=> BC^2 = 5^2 + 7^2 = 74
=> BC = căn bậc 2 của 74
b)
Xét tam giác ABE; tam giác DBE có :
AB = DB ( gt)
góc ABE = góc DBE ( gt)
BE chung
=> tam giác ABE = tam giác DBE (c.g.c) - đpcm
c)
Vì tam giác ABE = tam giác DBE (câu b)
=> AE = DE
Xét tg AEF ⊥ tại A; tg DEC ⊥ tại D:
AE = DE (c/m trên)
g AEF = g DEC (đối đỉnh)
=> tg AEF = tg DEC (cgv - gn) - đpcm
=> EF = EC
d)
Do tam giác AEF = tam giác DEC (câu c)
=> AE = DE
=> E ∈ đường trung trực của AD (1)
Lại do AB = BD (gt)
=> B ∈ đường trung trực của AD (2)
Từ (1) và (2) => BE là đường trung trực của AD. - đpcm

Câu hỏi của Nguyễn Thành Nam - Toán lớp 7 - Học toán với OnlineMath
Em tham khảo tại link trên nhé.

Bạn tham khảo ở đây nhé!!
https://h.vn/hoi-dap/question/536969.html
hok tốt!!
Bạn hỏi như vậy thì chắc có lẽ làm được câu a , b , c rồi , mình sẽ giải câu b ý 2
Hình bạn tự kẻ nha
Xét tam giác MDI và tam giác NEI có :
góc DMI = góc ENI (so le trong , MD song song với EN)
DM = EN (câu a)
góc MDI = góc NEI ( cùng bằng 90 dộ)
=> tam giác MDI = tam giác NEI
=> DI = EI
=> DI = IC + EC
Ta có : BC = BD + DI + IC . Mà DI = IC + EC
=> BC = BD + IC + EC + IC . Mà BD = EC ( giả thiết)
=> BC = EC + IC + EC + IC
=> BC = 2(EC + IC)
=> BC = 2 EI
Xét tam giác vuông IEN vuông tại E có : IN là cạnh huyền
=> IN > EI hay EI < IN
=> 2 EI < 2 IN
=> BC < MN ( vì MN = 2 IN do I là trung điểm MN)
Học tốt

b) Xét \(\Delta DMI\) và \(\Delta ENI\): \(\widehat{D}=\widehat{E}=90^0,MD=NE\) ( chứng minh câu a, bạn làm rồi nhé )
\(\widehat{MID}=\widehat{NIE}\) ( Hai góc đối đỉnh )
\(\Rightarrow MI=NI\)
c) Từ B và C kẻ các đường thẳng lần lượt vuông góc với AB và AC cắt nhau tại J.
Ta có: \(\Delta ABJ=\Delta ACJ\left(g-c-g\right)\Rightarrow JB=JC\)
Nên J thuộc AL đường trung trực ứng với cạnh BC.
Mặt khác: Từ \(\Delta DMB=\Delta ENC\) ( câu a )
Ta có: BM = CN; BJ = CJ ( cmt )
\(\widehat{MBJ}=\widehat{NCJ=90^o}\)
Nên \(\Delta BMJ=\Delta CNJ\left(c-g-c\right)\)
\(\Rightarrow MJ=NJ\) hay là đường trung trực của MN luôn đi qua điểm J cố định.

Bn tham khảo ở đây nha : https://olm.vn/hoi-dap/detail/86073517597.html

a: AC=12cm
b: Xét ΔABE vuông tại A và ΔDBE vuông tại D có
BE chung
BA=BD
Do đó: ΔABE=ΔDBE
c: Xét ΔAEK vuông tại A và ΔDEC vuông tại D có
EA=ED
\(\widehat{AEK}=\widehat{DEC}\)
Do đó: ΔAEK=ΔDEC
Suy ra:EK=EC
suy ra tam giác vuông cần thêm vuông theo định lí nào chứ bạn?