K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
27 tháng 6 2021
Bài 3 :
\(\Leftrightarrow\sqrt{9x^2-6x+1}=\sqrt{\left(3x-1\right)^2}=\left|3x-1\right|=5\)
\(\Leftrightarrow\left[{}\begin{matrix}3x-1=5\\3x-1=-5\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-\dfrac{4}{3}\end{matrix}\right.\)
Vậy ...
Bài 5 :
Ta có :\(x-5\sqrt{x}+7=x-2.\sqrt{x}.\dfrac{5}{2}+\dfrac{25}{4}+\dfrac{3}{4}=\left(\sqrt{x}-\dfrac{5}{2}\right)^2+\dfrac{3}{4}\)
Thấy : \(\left(\sqrt{x}-\dfrac{5}{2}\right)^2\ge0\)
\(\Rightarrow\left(\sqrt{x}-\dfrac{5}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\)
\(\Rightarrow P=\dfrac{1}{x-5\sqrt{x}+7}=\dfrac{1}{\left(\sqrt{x}-\dfrac{5}{2}\right)^2+\dfrac{3}{4}}\le\dfrac{1}{\dfrac{3}{4}}=\dfrac{4}{3}\)
Vậy \(Max_P=\dfrac{4}{3}\Leftrightarrow\sqrt{x}-\dfrac{5}{2}=0\Leftrightarrow x=\dfrac{25}{4}\)
27 tháng 6 2021
Bài 1:
a) Ta có: \(\sqrt{25}\cdot\sqrt{144}+\sqrt[3]{-27}-\sqrt[3]{216}\)
\(=5\cdot12-3-6\)
\(=60-9=51\)
b) Ta có: \(\sqrt{8.1\cdot360}\)
\(=\sqrt{8.1\cdot10\cdot36}\)
\(=\sqrt{81\cdot36}\)
\(=9\cdot6=54\)
Bài 2:
a) Ta có: \(\sqrt{80}-\sqrt{\left(2-\sqrt{5}\right)^2}+\sqrt{3\dfrac{1}{5}}\)
\(=4\sqrt{5}-\sqrt{5}+2+\dfrac{4}{\sqrt{5}}\)
\(=3\sqrt{5}+2+\dfrac{4\sqrt{5}}{5}\)
\(=\dfrac{10+19\sqrt{5}}{5}\)
b) Ta có: \(\dfrac{\sqrt{6}-\sqrt{3}}{1-\sqrt{2}}+\dfrac{3+6\sqrt{3}}{\sqrt{3}}-\dfrac{13}{\sqrt{3}+4}\)
\(=\dfrac{-\sqrt{3}\left(1-\sqrt{2}\right)}{1-\sqrt{2}}+\dfrac{\sqrt{3}\left(\sqrt{3}+6\right)}{\sqrt{3}}-\dfrac{13\left(4-\sqrt{3}\right)}{\left(4+\sqrt{3}\right)\left(4-\sqrt{3}\right)}\)
\(=-\sqrt{3}+\sqrt{3}+6-4+\sqrt{3}\)
\(=2+\sqrt{3}\)
TL
1
P
1
AT
23 tháng 6 2021
1. \(\dfrac{2}{2-\sqrt{3}}=\dfrac{2\left(2+\sqrt{3}\right)}{\left(2-\sqrt{3}\right)\left(2+\sqrt{3}\right)}=\dfrac{4+2\sqrt{3}}{2^2-\left(\sqrt{3}\right)^2}=\dfrac{4+2\sqrt{3}}{4-3}=4+2\sqrt{3}\)
2. \(\dfrac{1}{\sqrt{3}+\sqrt{2}}=\dfrac{\sqrt{3}-\sqrt{2}}{\left(\sqrt{3}+\sqrt{2}\right)\left(\sqrt{3}-\sqrt{2}\right)}=\dfrac{\sqrt{3}-\sqrt{2}}{\left(\sqrt{3}\right)^2-\left(\sqrt{2}\right)^2}=\dfrac{\sqrt{3}-\sqrt{2}}{3-2}\)
\(=\sqrt{3}-\sqrt{2}\)
3. \(\dfrac{1}{\sqrt{5}+\sqrt{7}}=\dfrac{\sqrt{7}-\sqrt{5}}{\left(\sqrt{5}+\sqrt{7}\right)\left(\sqrt{7}-\sqrt{5}\right)}=\dfrac{\sqrt{7}-\sqrt{5}}{\left(\sqrt{7}\right)^2-\left(\sqrt{5}\right)^2}=\dfrac{\sqrt{7}-\sqrt{5}}{7-5}\)
\(=\dfrac{\sqrt{7}-\sqrt{5}}{2}\)
4. \(\dfrac{1}{5-2\sqrt{6}}=\dfrac{5+2\sqrt{6}}{\left(5-2\sqrt{6}\right)\left(5+2\sqrt{6}\right)}=\dfrac{5+2\sqrt{6}}{5^2-\left(2\sqrt{6}\right)^2}=\dfrac{5+2\sqrt{6}}{25-24}\)
\(=5+2\sqrt{6}\)
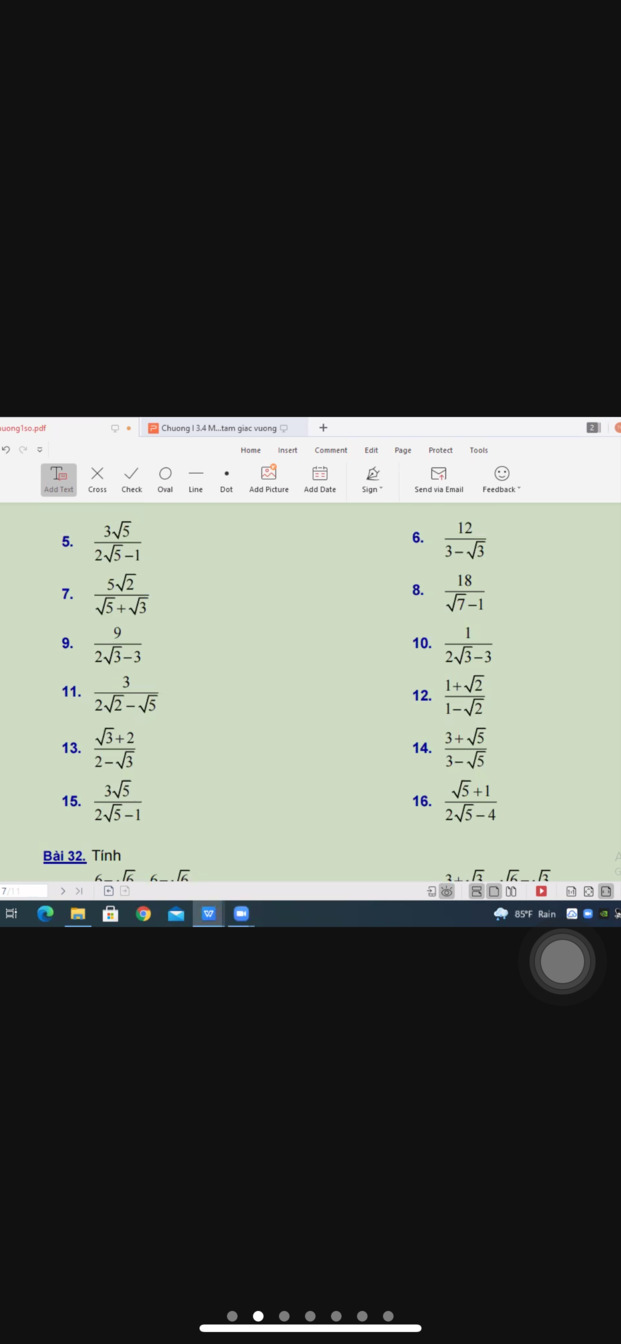
5. \(\dfrac{3\sqrt{5}}{2\sqrt{5}-1}=\dfrac{3\sqrt{5}\left(2\sqrt{5}+1\right)}{\left(2\sqrt{5}-1\right)\left(2\sqrt{5}\right)+1}=\dfrac{30+3\sqrt{5}}{\left(2\sqrt{5}\right)^2-1^2}=\dfrac{30+3\sqrt{5}}{20-1}\)
\(=\dfrac{30+3\sqrt{5}}{19}\)
6. \(\dfrac{12}{3-\sqrt{3}}=\dfrac{12}{\sqrt{3}\left(\sqrt{3}-1\right)}=\dfrac{4\sqrt{3}}{\sqrt{3}-1}=\dfrac{4\sqrt{3}\left(\sqrt{3}+1\right)}{\left(\sqrt{3}-1\right)\left(\sqrt{3}+1\right)}\)
\(\dfrac{12+4\sqrt{3}}{\left(\sqrt{3}\right)^2-1^2}=\dfrac{2\left(6+2\sqrt{3}\right)}{3-1}=6+2\sqrt{3}\)
7. \(\dfrac{5\sqrt{2}}{\sqrt{5}+\sqrt{3}}=\dfrac{5\sqrt{2}\left(\sqrt{5}-\sqrt{3}\right)}{\left(\sqrt{5}+\sqrt{3}\right)\left(\sqrt{5}-\sqrt{3}\right)}=\dfrac{5\sqrt{10}-5\sqrt{6}}{\left(\sqrt{5}\right)^2-\left(\sqrt{3}\right)^2}\)
\(=\dfrac{5\sqrt{10}-5\sqrt{6}}{5-3}=\dfrac{5\sqrt{10}-5\sqrt{6}}{2}\)
8. \(\dfrac{18}{\sqrt{7}-1}=\dfrac{18\left(\sqrt{7}+1\right)}{\left(\sqrt{7}-1\right)\left(\sqrt{7}+1\right)}=\dfrac{18\left(\sqrt{7}+1\right)}{\left(\sqrt{7}\right)^2-1^2}=\dfrac{18\left(\sqrt{7}+1\right)}{7-1}\)
\(=3\left(\sqrt{7}+1\right)=3\sqrt{7}+3\)
9. \(\dfrac{9}{2\sqrt{3}-3}=\dfrac{9\left(2\sqrt{3}+3\right)}{\left(2\sqrt{3}-3\right)\left(2\sqrt{3}+3\right)}=\dfrac{9\left(2\sqrt{3}+3\right)}{\left(2\sqrt{3}\right)^2-3^2}=\dfrac{9\left(2\sqrt{3}+3\right)}{12-9}\)
\(3\left(2\sqrt{3}+3\right)=6\sqrt{3}+9\)
10. \(\dfrac{1}{2\sqrt{3}-3}=\dfrac{2\sqrt{3}+3}{\left(2\sqrt{3}-3\right)\left(2\sqrt{3}+3\right)}=\dfrac{2\sqrt{3}+3}{\left(2\sqrt{3}\right)^2-3^2}=\dfrac{2\sqrt{3}+3}{12-9}\)
\(=\dfrac{2\sqrt{3}+3}{3}\)
11. \(\dfrac{3}{2\sqrt{2}-\sqrt{5}}=\dfrac{3\left(2\sqrt{2}+\sqrt{5}\right)}{\left(2\sqrt{2}-\sqrt{5}\right)\left(2\sqrt{2}+\sqrt{5}\right)}=\dfrac{3\left(2\sqrt{2}+\sqrt{5}\right)}{\left(2\sqrt{2}\right)^2-\left(\sqrt{5}\right)^2}\)
\(=\dfrac{3\left(2\sqrt{2}+\sqrt{5}\right)}{8-5}=2\sqrt{2}+5\)
12. \(\dfrac{1+\sqrt{2}}{1-\sqrt{2}}=\dfrac{\left(1+\sqrt{2}\right)\left(1+\sqrt{2}\right)}{\left(1-\sqrt{2}\right)\left(1+\sqrt{2}\right)}=\dfrac{\left(1+\sqrt{2}\right)^2}{1^2-\left(\sqrt{2}\right)^2}=\dfrac{3+2\sqrt{2}}{-1}\)
\(=-3-2\sqrt{2}\)
13. \(\dfrac{\sqrt{3}+2}{2-\sqrt{3}}=\dfrac{\left(\sqrt{3}+2\right)\left(\sqrt{3}+2\right)}{\left(2-\sqrt{3}\right)\left(2+\sqrt{3}\right)}=\dfrac{\left(\sqrt{3}+2\right)^2}{2^2-\left(\sqrt{3}\right)^2}=\dfrac{7+4\sqrt{3}}{4-3}=7+4\sqrt{3}\)
14. \(\dfrac{3+\sqrt{5}}{3-\sqrt{5}}=\dfrac{\left(3+\sqrt{5}\right)\left(3+\sqrt{5}\right)}{\left(3-\sqrt{5}\right)\left(3+\sqrt{5}\right)}=\dfrac{\left(3+\sqrt{5}\right)^2}{3^2-\left(\sqrt{5}\right)^2}=\dfrac{14+6\sqrt{5}}{9-5}\)
\(=\dfrac{7+3\sqrt{5}}{2}\)
15. giống câu 5
16. \(\dfrac{\sqrt{5}+1}{2\sqrt{5}-4}=\dfrac{\left(\sqrt{5}+1\right)\left(2\sqrt{5}+4\right)}{\left(2\sqrt{5}-4\right)\left(2\sqrt{5}+4\right)}=\dfrac{14+6\sqrt{5}}{\left(2\sqrt{5}\right)^2-4^2}=\dfrac{14+6\sqrt{5}}{4}\)
\(=\dfrac{7+3\sqrt{5}}{2}\)
23 tháng 6 2021
- Sử dụng liên hợp thôi nha mình làm tham khảo câu 1, 4 các câu khác tương tự .
\(1,\dfrac{2}{2-\sqrt{3}}=\dfrac{2\left(2+\sqrt{3}\right)}{\left(2-\sqrt{3}\right)\left(2+\sqrt{3}\right)}=\dfrac{4+2\sqrt{3}}{4-3}=3+2\sqrt{3}+1=\left(\sqrt{3}+1\right)^2\)
\(4,\dfrac{1}{5-2\sqrt{6}}=\dfrac{5+2\sqrt{6}}{5^2-\left(2\sqrt{6}\right)^2}=5+2\sqrt{6}\)
7 tháng 10 2021
Bài 2:
Xét ΔABC vuông tại C có
\(CB=BA\cdot\sin60^0=12\cdot\dfrac{\sqrt{3}}{2}=6\sqrt{3}\left(cm\right)\)
HT
0
25 tháng 8 2021
Bài 7:
a: Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHB vuông tại H có HE là đường cao ứng với cạnh huyền AB, ta được:
\(AE\cdot AB=AH^2\left(1\right)\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔHAC vuông tại H có HF là đường cao ứng với cạnh huyền AC, ta được:
\(AF\cdot AC=AH^2\left(2\right)\)
Từ (1), (2) suy ra \(AE\cdot AB=AF\cdot AC\)
Bài 2:
\(\sqrt{2x-1}=5\)
=> 2x - 1 = 25
=> 2x = 26
=> x = 13
b) \(\sqrt[3]{3x+2}=-3\)
=> 3x + 2 = -27
=> 3x = -29
=> x = -29/3
P/s: Mỗi lần chỉ đc hỏi 1 bài thôi em nehs!
1. ĐK:
a, \(x\ge\dfrac{5}{2}\)
b, \(\left\{{}\begin{matrix}x\ge0\\x\ne\dfrac{9}{4}\end{matrix}\right.\)
2.
a,ĐK: \(x\ge\dfrac{1}{2}\)
PT\(\Leftrightarrow2x-1=25\Rightarrow x=13\left(tm\right)\)
b,ĐK: \(\forall x\in R\)
PT\(\Leftrightarrow3x+2=-27=>x=-\dfrac{29}{3}\) (tm)
3.
a,\(\sqrt{5}.\sqrt{1,2}.\sqrt{24}=\sqrt{120}.\sqrt{1,2}=12\)
b,\(\dfrac{\sqrt{4444}}{\sqrt{1111}}=\dfrac{\sqrt{4}.\sqrt{1111}}{\sqrt{1111}}=2\)
c,\(\sqrt{\dfrac{3}{5}}+\sqrt{\dfrac{5}{3}}-\dfrac{1}{2}\sqrt{60}=\dfrac{8}{\sqrt{15}}-\sqrt{15}=-\dfrac{7}{\sqrt{15}}\)
d,\(\sqrt{5+2\sqrt{6}}+\sqrt{5-2\sqrt{6}}=\sqrt{3}+\sqrt{2}+\sqrt{3}-\sqrt{2}=2\sqrt{3}\)