
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 14:
a)
Sửa đề: \(AE\cdot AB=AD\cdot AC\)
Xét ΔADB vuông tại D và ΔAEC vuông tại E có
\(\widehat{BAD}\) chung
Do đó: ΔADB\(\sim\)ΔAEC(g-g)
Suy ra: \(\dfrac{AD}{AE}=\dfrac{AB}{AC}\)
hay \(AE\cdot AB=AD\cdot AC\)(đpcm)
b) Ta có: \(\dfrac{AD}{AE}=\dfrac{AB}{AC}\)(cmt)
nên \(\dfrac{AD}{AB}=\dfrac{AE}{AC}\)
Xét ΔADB vuông tại D có
\(\cos\widehat{A}=\dfrac{AD}{AB}\)
Xét ΔAED và ΔACB có
\(\dfrac{AD}{AB}=\dfrac{AE}{AC}\)(cmt)
\(\widehat{A}\) chung
Do đó: ΔAED∼ΔACB(c-g-c)
Suy ra: \(\dfrac{AD}{AB}=\dfrac{ED}{CB}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(\dfrac{AD}{AB}\cdot BC=DE\)
\(\Leftrightarrow DE=BC\cdot\cos\widehat{A}\)(đpcm)
c) Ta có: \(DE=BC\cdot\cos\widehat{A}\)(cmt)
nên \(DE=BC\cdot\cos60^0=\dfrac{1}{2}BC\)(1)
Ta có: ΔEBC vuông tại E(gt)
mà EM là đường trung tuyến ứng với cạnh huyền BC(M là trung điểm của BC)
nên \(EM=\dfrac{1}{2}BC\)(2)
Ta có: ΔDBC vuông tại D(gt)
mà DM là đường trung tuyến ứng với cạnh huyền BC(M là trung điểm của BC)
nên \(DM=\dfrac{1}{2}BC\)(3)
Từ (1), (2) và (3) suy ra ME=MD=DE
hay ΔMDE đều(đpcm)

Bài 2:
Xét ΔABC vuông tại C có
\(CB=BA\cdot\sin60^0=12\cdot\dfrac{\sqrt{3}}{2}=6\sqrt{3}\left(cm\right)\)

Bài IV:
1: Xét tứ giác MAOB có
\(\widehat{MAO}+\widehat{MBO}=90^0+90^0=180^0\)
=>MAOB là tứ giác nội tiếp
=>M,A,O,B cùng thuộc một đường tròn
2: Xét (O) có
MA,MB là các tiếp tuyến
Do đó: MA=MB
=>M nằm trên đường trung trực của AB(1)
Ta có: OA=OB
=>O nằm trên đường trung trực của AB(2)
Từ (1) và (2) suy ra MO là đường trung trực của BA
=>MO\(\perp\)AB tại H và H là trung điểm của AB
Xét ΔMAO vuông tại A có AH là đường cao
nên \(MH\cdot MO=MA^2\left(3\right)\)
Xét (O) có
ΔACD nội tiếp
AD là đường kính
Do đó: ΔACD vuông tại C
=>AC\(\perp\)CD tại C
=>AC\(\perp\)DM tại C
Xét ΔADM vuông tại A có AC là đường cao
nên \(MC\cdot MD=MA^2\left(4\right)\)
Từ (3) và (4) suy ra \(MA^2=MH\cdot MO=MC\cdot MD\)
3: Ta có: \(\widehat{MAI}+\widehat{OAI}=\widehat{OAM}=90^0\)
\(\widehat{HAI}+\widehat{OIA}=90^0\)(ΔAHI vuông tại H)
mà \(\widehat{OAI}=\widehat{OIA}\)
nên \(\widehat{MAI}=\widehat{HAI}\)
=>AI là phân giác của góc HAM
Xét ΔAHM có AI là phân giác
nên \(\dfrac{HI}{IM}=\dfrac{AH}{AM}\left(5\right)\)
Xét ΔOHA vuông tại H và ΔOAM vuông tại A có
\(\widehat{HOA}\) chung
Do đó: ΔOHA đồng dạng với ΔOAM
=>\(\dfrac{OH}{OA}=\dfrac{HA}{AM}\)
=>\(\dfrac{OH}{OI}=\dfrac{AH}{AM}\left(6\right)\)
Từ (5) và (6) suy ra \(\dfrac{OH}{OI}=\dfrac{IH}{IM}\)
=>\(HO\cdot IM=IO\cdot IH\)

Công thức đây nhé (Áp dụng làm thử đi)
Tỉ số giữa cạnh đối và cạnh huyền được gọi là sin của góc , kí hiệu .Tỉ số giữa cạnh kề và cạnh huyền được gọi là côsin của góc , kí hiệu .
Tỉ số giữa cạnh đối và cạnh kề được gọi là tang của góc , kí hiệu .
Tỉ số giữa cạnh kề và cạnh đối gọi là côtang của góc , kí hiệu .

Bài 2:
\(\sqrt{2x-1}=5\)
=> 2x - 1 = 25
=> 2x = 26
=> x = 13
b) \(\sqrt[3]{3x+2}=-3\)
=> 3x + 2 = -27
=> 3x = -29
=> x = -29/3
P/s: Mỗi lần chỉ đc hỏi 1 bài thôi em nehs!
1. ĐK:
a, \(x\ge\dfrac{5}{2}\)
b, \(\left\{{}\begin{matrix}x\ge0\\x\ne\dfrac{9}{4}\end{matrix}\right.\)
2.
a,ĐK: \(x\ge\dfrac{1}{2}\)
PT\(\Leftrightarrow2x-1=25\Rightarrow x=13\left(tm\right)\)
b,ĐK: \(\forall x\in R\)
PT\(\Leftrightarrow3x+2=-27=>x=-\dfrac{29}{3}\) (tm)
3.
a,\(\sqrt{5}.\sqrt{1,2}.\sqrt{24}=\sqrt{120}.\sqrt{1,2}=12\)
b,\(\dfrac{\sqrt{4444}}{\sqrt{1111}}=\dfrac{\sqrt{4}.\sqrt{1111}}{\sqrt{1111}}=2\)
c,\(\sqrt{\dfrac{3}{5}}+\sqrt{\dfrac{5}{3}}-\dfrac{1}{2}\sqrt{60}=\dfrac{8}{\sqrt{15}}-\sqrt{15}=-\dfrac{7}{\sqrt{15}}\)
d,\(\sqrt{5+2\sqrt{6}}+\sqrt{5-2\sqrt{6}}=\sqrt{3}+\sqrt{2}+\sqrt{3}-\sqrt{2}=2\sqrt{3}\)

b: \(BC=\sqrt{89}\left(cm\right)\)
\(\sin\widehat{B}=\dfrac{5\sqrt{89}}{89}\)
\(\Leftrightarrow\widehat{B}\simeq32^0\)
\(\widehat{C}=58^0\)















1. \(\dfrac{2}{2-\sqrt{3}}=\dfrac{2\left(2+\sqrt{3}\right)}{\left(2-\sqrt{3}\right)\left(2+\sqrt{3}\right)}=\dfrac{4+2\sqrt{3}}{2^2-\left(\sqrt{3}\right)^2}=\dfrac{4+2\sqrt{3}}{4-3}=4+2\sqrt{3}\)
2. \(\dfrac{1}{\sqrt{3}+\sqrt{2}}=\dfrac{\sqrt{3}-\sqrt{2}}{\left(\sqrt{3}+\sqrt{2}\right)\left(\sqrt{3}-\sqrt{2}\right)}=\dfrac{\sqrt{3}-\sqrt{2}}{\left(\sqrt{3}\right)^2-\left(\sqrt{2}\right)^2}=\dfrac{\sqrt{3}-\sqrt{2}}{3-2}\)
\(=\sqrt{3}-\sqrt{2}\)
3. \(\dfrac{1}{\sqrt{5}+\sqrt{7}}=\dfrac{\sqrt{7}-\sqrt{5}}{\left(\sqrt{5}+\sqrt{7}\right)\left(\sqrt{7}-\sqrt{5}\right)}=\dfrac{\sqrt{7}-\sqrt{5}}{\left(\sqrt{7}\right)^2-\left(\sqrt{5}\right)^2}=\dfrac{\sqrt{7}-\sqrt{5}}{7-5}\)
\(=\dfrac{\sqrt{7}-\sqrt{5}}{2}\)
4. \(\dfrac{1}{5-2\sqrt{6}}=\dfrac{5+2\sqrt{6}}{\left(5-2\sqrt{6}\right)\left(5+2\sqrt{6}\right)}=\dfrac{5+2\sqrt{6}}{5^2-\left(2\sqrt{6}\right)^2}=\dfrac{5+2\sqrt{6}}{25-24}\)
\(=5+2\sqrt{6}\)
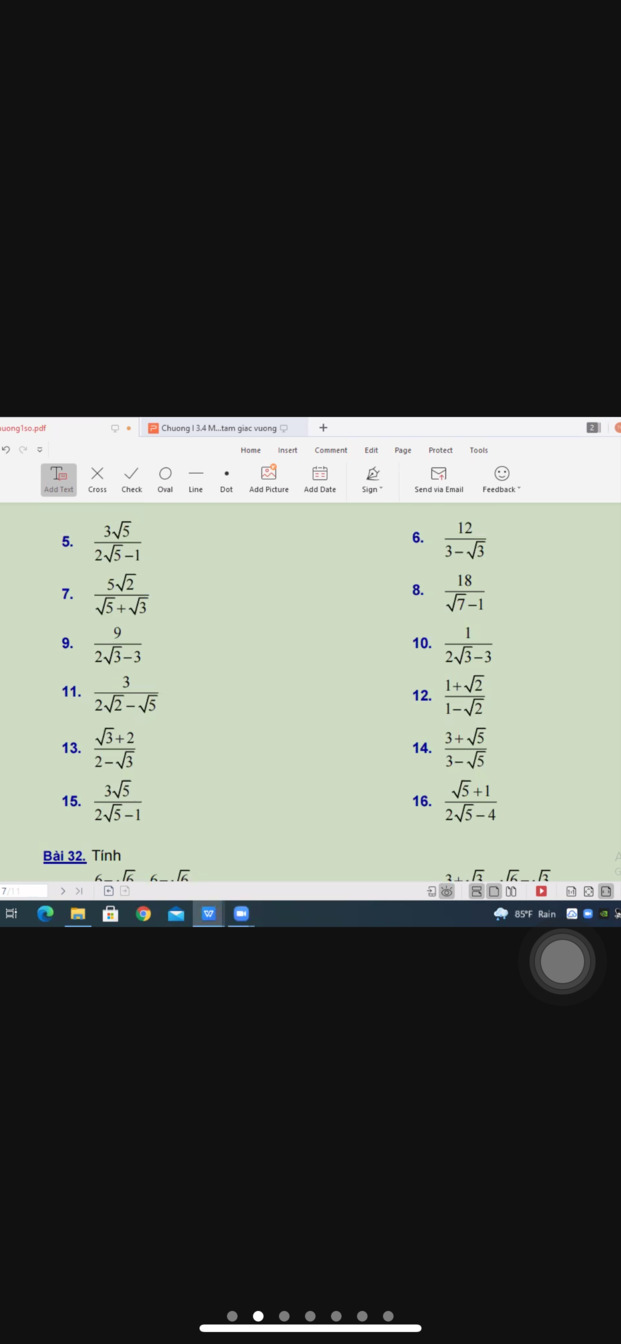
5. \(\dfrac{3\sqrt{5}}{2\sqrt{5}-1}=\dfrac{3\sqrt{5}\left(2\sqrt{5}+1\right)}{\left(2\sqrt{5}-1\right)\left(2\sqrt{5}\right)+1}=\dfrac{30+3\sqrt{5}}{\left(2\sqrt{5}\right)^2-1^2}=\dfrac{30+3\sqrt{5}}{20-1}\)
\(=\dfrac{30+3\sqrt{5}}{19}\)
6. \(\dfrac{12}{3-\sqrt{3}}=\dfrac{12}{\sqrt{3}\left(\sqrt{3}-1\right)}=\dfrac{4\sqrt{3}}{\sqrt{3}-1}=\dfrac{4\sqrt{3}\left(\sqrt{3}+1\right)}{\left(\sqrt{3}-1\right)\left(\sqrt{3}+1\right)}\)
\(\dfrac{12+4\sqrt{3}}{\left(\sqrt{3}\right)^2-1^2}=\dfrac{2\left(6+2\sqrt{3}\right)}{3-1}=6+2\sqrt{3}\)
7. \(\dfrac{5\sqrt{2}}{\sqrt{5}+\sqrt{3}}=\dfrac{5\sqrt{2}\left(\sqrt{5}-\sqrt{3}\right)}{\left(\sqrt{5}+\sqrt{3}\right)\left(\sqrt{5}-\sqrt{3}\right)}=\dfrac{5\sqrt{10}-5\sqrt{6}}{\left(\sqrt{5}\right)^2-\left(\sqrt{3}\right)^2}\)
\(=\dfrac{5\sqrt{10}-5\sqrt{6}}{5-3}=\dfrac{5\sqrt{10}-5\sqrt{6}}{2}\)
8. \(\dfrac{18}{\sqrt{7}-1}=\dfrac{18\left(\sqrt{7}+1\right)}{\left(\sqrt{7}-1\right)\left(\sqrt{7}+1\right)}=\dfrac{18\left(\sqrt{7}+1\right)}{\left(\sqrt{7}\right)^2-1^2}=\dfrac{18\left(\sqrt{7}+1\right)}{7-1}\)
\(=3\left(\sqrt{7}+1\right)=3\sqrt{7}+3\)
9. \(\dfrac{9}{2\sqrt{3}-3}=\dfrac{9\left(2\sqrt{3}+3\right)}{\left(2\sqrt{3}-3\right)\left(2\sqrt{3}+3\right)}=\dfrac{9\left(2\sqrt{3}+3\right)}{\left(2\sqrt{3}\right)^2-3^2}=\dfrac{9\left(2\sqrt{3}+3\right)}{12-9}\)
\(3\left(2\sqrt{3}+3\right)=6\sqrt{3}+9\)
10. \(\dfrac{1}{2\sqrt{3}-3}=\dfrac{2\sqrt{3}+3}{\left(2\sqrt{3}-3\right)\left(2\sqrt{3}+3\right)}=\dfrac{2\sqrt{3}+3}{\left(2\sqrt{3}\right)^2-3^2}=\dfrac{2\sqrt{3}+3}{12-9}\)
\(=\dfrac{2\sqrt{3}+3}{3}\)
11. \(\dfrac{3}{2\sqrt{2}-\sqrt{5}}=\dfrac{3\left(2\sqrt{2}+\sqrt{5}\right)}{\left(2\sqrt{2}-\sqrt{5}\right)\left(2\sqrt{2}+\sqrt{5}\right)}=\dfrac{3\left(2\sqrt{2}+\sqrt{5}\right)}{\left(2\sqrt{2}\right)^2-\left(\sqrt{5}\right)^2}\)
\(=\dfrac{3\left(2\sqrt{2}+\sqrt{5}\right)}{8-5}=2\sqrt{2}+5\)
12. \(\dfrac{1+\sqrt{2}}{1-\sqrt{2}}=\dfrac{\left(1+\sqrt{2}\right)\left(1+\sqrt{2}\right)}{\left(1-\sqrt{2}\right)\left(1+\sqrt{2}\right)}=\dfrac{\left(1+\sqrt{2}\right)^2}{1^2-\left(\sqrt{2}\right)^2}=\dfrac{3+2\sqrt{2}}{-1}\)
\(=-3-2\sqrt{2}\)
13. \(\dfrac{\sqrt{3}+2}{2-\sqrt{3}}=\dfrac{\left(\sqrt{3}+2\right)\left(\sqrt{3}+2\right)}{\left(2-\sqrt{3}\right)\left(2+\sqrt{3}\right)}=\dfrac{\left(\sqrt{3}+2\right)^2}{2^2-\left(\sqrt{3}\right)^2}=\dfrac{7+4\sqrt{3}}{4-3}=7+4\sqrt{3}\)
14. \(\dfrac{3+\sqrt{5}}{3-\sqrt{5}}=\dfrac{\left(3+\sqrt{5}\right)\left(3+\sqrt{5}\right)}{\left(3-\sqrt{5}\right)\left(3+\sqrt{5}\right)}=\dfrac{\left(3+\sqrt{5}\right)^2}{3^2-\left(\sqrt{5}\right)^2}=\dfrac{14+6\sqrt{5}}{9-5}\)
\(=\dfrac{7+3\sqrt{5}}{2}\)
15. giống câu 5
16. \(\dfrac{\sqrt{5}+1}{2\sqrt{5}-4}=\dfrac{\left(\sqrt{5}+1\right)\left(2\sqrt{5}+4\right)}{\left(2\sqrt{5}-4\right)\left(2\sqrt{5}+4\right)}=\dfrac{14+6\sqrt{5}}{\left(2\sqrt{5}\right)^2-4^2}=\dfrac{14+6\sqrt{5}}{4}\)
\(=\dfrac{7+3\sqrt{5}}{2}\)
- Sử dụng liên hợp thôi nha mình làm tham khảo câu 1, 4 các câu khác tương tự .
\(1,\dfrac{2}{2-\sqrt{3}}=\dfrac{2\left(2+\sqrt{3}\right)}{\left(2-\sqrt{3}\right)\left(2+\sqrt{3}\right)}=\dfrac{4+2\sqrt{3}}{4-3}=3+2\sqrt{3}+1=\left(\sqrt{3}+1\right)^2\)
\(4,\dfrac{1}{5-2\sqrt{6}}=\dfrac{5+2\sqrt{6}}{5^2-\left(2\sqrt{6}\right)^2}=5+2\sqrt{6}\)