K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
H
25 tháng 5 2023
c. Dễ chứng minh 5 điểm A, N, F, H, E cùng thuộc đường tròn đường kính AH.
\(\Rightarrow HN\perp AN\left(1\right)\)
Vẽ đường kính AM của (O) \(\Rightarrow MN\perp AN\left(2\right)\)
Từ (1), (2) suy ra 3 điểm M, H, N thẳng hàng (3)
Dễ chứng minh BHCM là hình bình hành (BH // CM do cùng vuông góc với AC, tương tự 2 cạnh còn lại)
\(\Rightarrow\) 3 điểm H, I, M thẳng hàng (4)
Từ (3), (4) suy ra 3 điểm N, H, I thẳng hàng.
24 tháng 10 2021
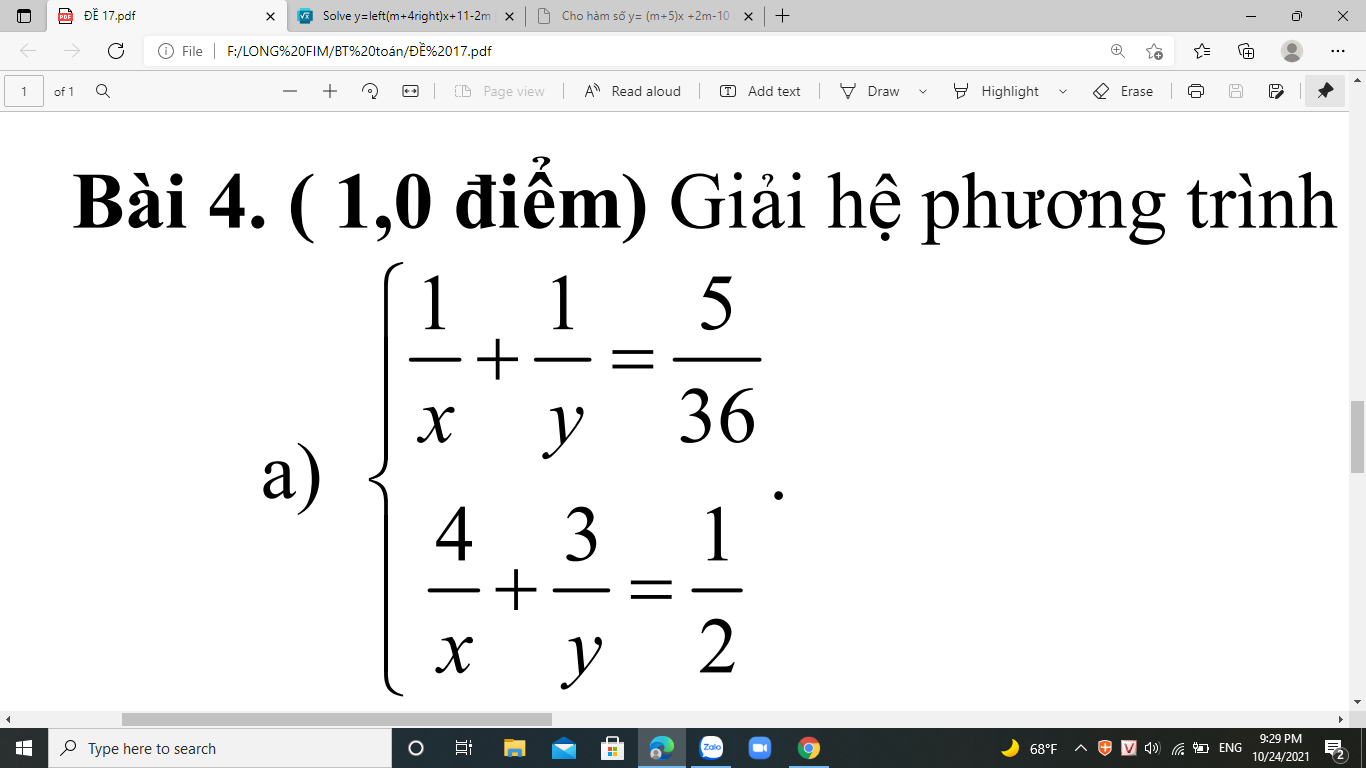
\(\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{5}{36}\\\dfrac{4}{x}+\dfrac{3}{y}=\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{4}{x}+\dfrac{4}{y}=\dfrac{5}{9}\\\dfrac{4}{x}+\dfrac{3}{y}=\dfrac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{y}=\dfrac{1}{18}\\\dfrac{1}{x}=\dfrac{1}{36}-\dfrac{1}{18}=-\dfrac{1}{36}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=18\\x=-36\end{matrix}\right.\)
24 tháng 1 2022
c: \(\widehat{FDH}=\widehat{ABE}\)
\(\widehat{EDH}=\widehat{ACF}\)
mà \(\widehat{ABE}=\widehat{ACF}\)
nên DH là tia phân giác của góc EDF
\(\widehat{FEH}=\widehat{BAD}\)
\(\widehat{DEH}=\widehat{FCB}\)
mà \(\widehat{BAD}=\widehat{FCB}\)
nên EH là tia phân giác của góc DEF
ai biết phần c làm như thế nào ko ạ
14 tháng 11 2021
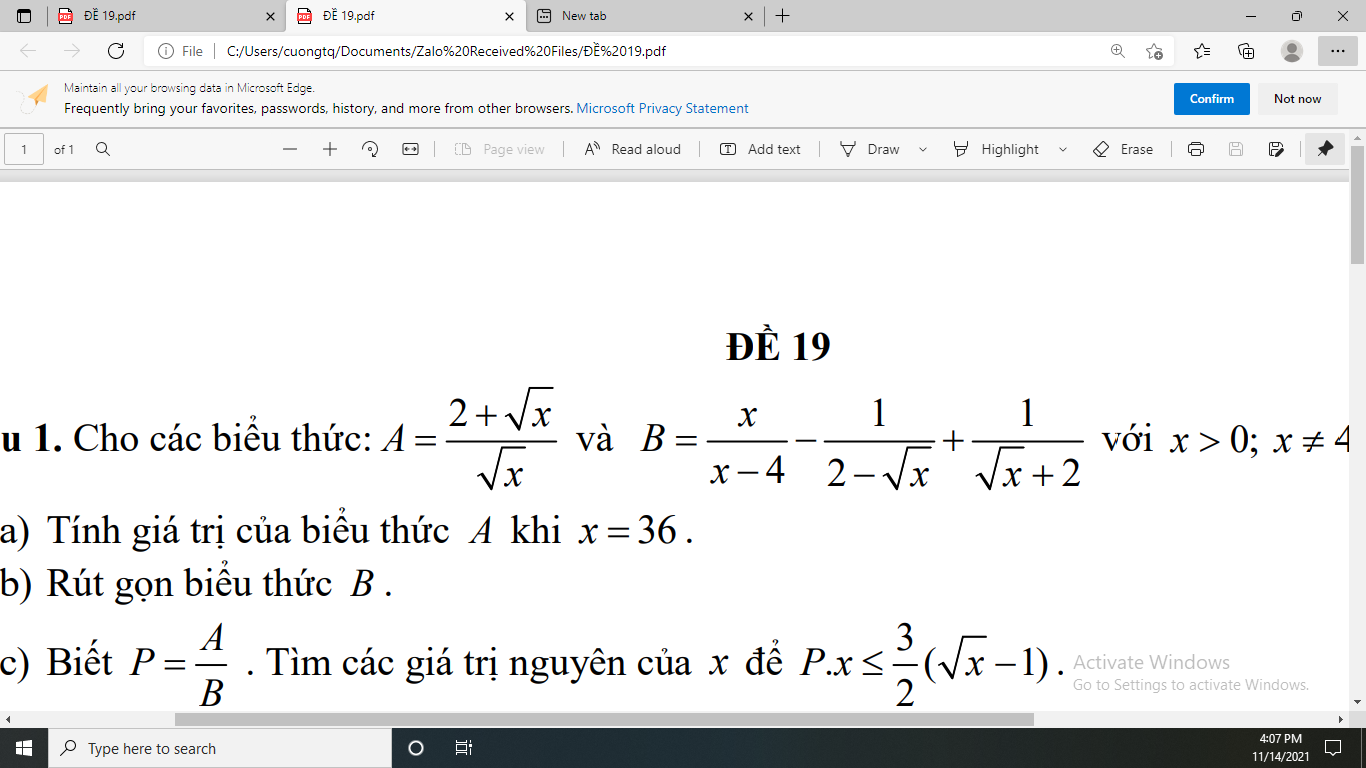
\(a,A=\dfrac{2+6}{6}=\dfrac{8}{6}=\dfrac{4}{3}\\ b,B=\dfrac{x+\sqrt{x}+2+\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{\sqrt{x}\left(\sqrt{x}+2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\\ B=\dfrac{\sqrt{x}}{\sqrt{x}-2}\\ c,P=\dfrac{A}{B}=\dfrac{2+\sqrt{x}}{\sqrt{x}}\cdot\dfrac{\sqrt{x}-2}{\sqrt{x}}=\dfrac{x-4}{x}\\ Px\le\dfrac{3}{2}\left(\sqrt{x}-1\right)\Leftrightarrow x-4\le\dfrac{3}{2}\left(\sqrt{x}-1\right)\\ \Leftrightarrow2x-8\le3\sqrt{x}-3\\ \Leftrightarrow2x-3\sqrt{x}-5\le0\\ \Leftrightarrow\left(2\sqrt{x}-5\right)\left(\sqrt{x}+1\right)\le0\\ \Leftrightarrow-1\le\sqrt{x}\le\dfrac{5}{2}\Leftrightarrow1\le x\le\dfrac{25}{4};x\ne4\)
NV
Nguyễn Việt Lâm
Giáo viên
26 tháng 3 2022
Pt hoành độ giao điểm: \(x^2-mx-m-1=0\) (1)
(d) cắt (P) tại 2 điểm pb nằm về 2 phía trục tung khi (1) có 2 nghiệm pb trái dấu
\(\Leftrightarrow ac=-m-1< 0\Rightarrow m>-1\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=m\\x_1x_2=-m-1\end{matrix}\right.\)
\(y_1+y_2=50\)
\(\Leftrightarrow\left(mx_1+m+1\right)+\left(mx_2+m+1\right)=50\)
\(\Leftrightarrow m\left(x_1+x_2\right)+2m-48=0\)
\(\Leftrightarrow m^2+2m-48=0\Rightarrow\left[{}\begin{matrix}m=6\\m=-8\left(loại\right)\end{matrix}\right.\)
11 tháng 3 2022
\(\Delta'=4-\left(m-1\right)=5-m\)
để pt có nghiệm kép khi \(5-m=0\Leftrightarrow m=5\)
chọn B
NV
Nguyễn Việt Lâm
Giáo viên
11 tháng 3 2022
Phương trình có nghiệm kép khi:
\(\Delta'=4-\left(m-1\right)=0\Leftrightarrow5-m=0\)
\(\Rightarrow m=5\)
3: Gọi I là điểm đối xứng của O qua BC, OI cắt BC tại N
=>N là trung điểm chung của OI và BC và I,N cố định
BH//CD; CH//BD
=>BHCD là hbh
=>N là trung điểm của HD
ON là đường trung bình của ΔAHD
=>AH=2ON
=>AH=OI=2ON
AH//OI
=>AHOI là hbh
=>IH=OA=R
=>H thuộc (I;R) cố định