Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔBAC có BA=BC và góc B=60 độ
nên ΔBAC đều
b: ΔBAC đều
mà AF là đường cao
nên AF là phân giác của góc BAC
=>góc FAC=góc FAB=60/2=30 độ
Xét ΔDAC có DA=DC và góc D=60 độ
nên ΔDAC đều
=>AE là phân giác của góc CAD
=>góc CAE=60/2=30 độ
góc CAE=góc CAF
=>AC là phân giác của góc FAE
c: Xét ΔAFC vuông tại F và ΔAEC vuông tại E có
góc FAC=góc EAC
AC chung
góc FCA=góc ECA
=>ΔAFC=ΔAEC
=>AF=AE
Xét ΔAFE có
AF=AE
góc FAE=60 độ
=>ΔAFE đều

a: Ta có: \(\widehat{BAM}+\widehat{DAM}=\widehat{BAD}=90^0\)
\(\widehat{MAD}+\widehat{NAD}=\widehat{MAN}=90^0\)
Do đó: \(\widehat{BAM}=\widehat{NAD}\)
Xét ΔABM vuông tại B và ΔADN vuông tại D có
AB=AD
\(\widehat{BAM}=\widehat{DAN}\)
Do đó: ΔABM=ΔADN
=>AM=AN

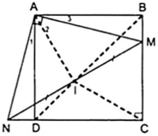
Áp dụng định nghĩa và giả thiết của hình vuông ABCD ta được:
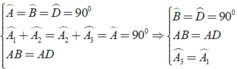
⇒ Δ ABM = Δ ADN( g - c - g )
Do đó AM = AN (cặp cạnh tương ứng bằng nhau)

a) △APQ và △BMQ có: \(\widehat{PAQ}=\widehat{MBQ}=45^0;\widehat{AQP}=\widehat{BQM}\).
\(\Rightarrow\)△APQ∼△BMQ (g-g)
\(\Rightarrow\dfrac{QP}{QM}=\dfrac{QA}{QB}\Rightarrow\dfrac{QP}{QA}=\dfrac{QM}{QB}\)
△ABQ và △PMQ có: \(\dfrac{QP}{QA}=\dfrac{QM}{QB};\widehat{AQB}=\widehat{PQM}\)
\(\Rightarrow\)△ABQ∼△PMQ (c-g-c).
b) △ABQ∼△PMQ \(\Rightarrow\dfrac{PM}{AB}=\dfrac{PQ}{AQ};\widehat{BAQ}=\widehat{MPQ}\Rightarrow MP=\dfrac{PQ}{AQ}.AB\)
△APQ và △BPA có: \(\widehat{QAP}=\widehat{ABP}=45^0;\widehat{APB}\) là góc chung.
\(\Rightarrow\)△APQ∼△BPA (g-g)
\(\Rightarrow\widehat{AQP}=\widehat{BAP}\)
\(\widehat{APM}=\widehat{APQ}+\widehat{MPQ}=180^0-45^0-\widehat{AQP}+\widehat{BAQ}=180^0-45^0-\left(\widehat{BAP}-\widehat{BAQ}\right)=180^0-45^0-45^0=90^0\)
\(\Rightarrow\)MP⊥AN tại P.
△MPN và △AHN có: \(\widehat{MPN}=\widehat{AHN}=90^0;\widehat{ANM}\) là góc chung.
\(\Rightarrow\)△MPN∼△AHN (g-g)
\(\Rightarrow\dfrac{AH}{MP}=\dfrac{AN}{MN};\dfrac{NP}{NH}=\dfrac{NM}{NA}\Rightarrow\dfrac{NP}{NM}=\dfrac{NH}{NA}\)
△APQ và △AMN có: \(\dfrac{NP}{NM}=\dfrac{NH}{NA};\widehat{MAN}\) là góc chung.
\(\Rightarrow\)△APQ∼△AMN (c-g-c)
\(\Rightarrow\dfrac{AQ}{AN}=\dfrac{PQ}{MN}\Rightarrow\dfrac{MN}{AN}=\dfrac{PQ}{AQ}\)
\(\dfrac{AH}{MP}=\dfrac{AN}{MN}\Rightarrow AH=MP.\dfrac{AN}{MN}=\dfrac{PQ}{AQ}.AB.\dfrac{AN}{AM}=AB\) không đổi.

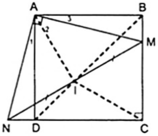
Ta có IA, IC lần lượt là các đường trung tuyến ứng với cạnh huyền của hai tam giác vuông AMN, CMN.
Áp dụng tính chất đường trung tuyến ứng vói cạnh huyền của hai tam giác vuông trên và định nghĩa ta có: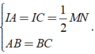
Chứng tỏ hai điểm B và I cách đều hai điểm A và C nên BI là đường trung trực của đoạn AC.
Mà theo tính chất của hình vuông thì BD là đường trung trực của AC mà đoạn AC chỉ có một đường trung trực nên BI trung với BD hay B,I,D thẳng hàng.