Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a) △APQ và △BMQ có: \(\widehat{PAQ}=\widehat{MBQ}=45^0;\widehat{AQP}=\widehat{BQM}\).
\(\Rightarrow\)△APQ∼△BMQ (g-g)
\(\Rightarrow\dfrac{QP}{QM}=\dfrac{QA}{QB}\Rightarrow\dfrac{QP}{QA}=\dfrac{QM}{QB}\)
△ABQ và △PMQ có: \(\dfrac{QP}{QA}=\dfrac{QM}{QB};\widehat{AQB}=\widehat{PQM}\)
\(\Rightarrow\)△ABQ∼△PMQ (c-g-c).
b) △ABQ∼△PMQ \(\Rightarrow\dfrac{PM}{AB}=\dfrac{PQ}{AQ};\widehat{BAQ}=\widehat{MPQ}\Rightarrow MP=\dfrac{PQ}{AQ}.AB\)
△APQ và △BPA có: \(\widehat{QAP}=\widehat{ABP}=45^0;\widehat{APB}\) là góc chung.
\(\Rightarrow\)△APQ∼△BPA (g-g)
\(\Rightarrow\widehat{AQP}=\widehat{BAP}\)
\(\widehat{APM}=\widehat{APQ}+\widehat{MPQ}=180^0-45^0-\widehat{AQP}+\widehat{BAQ}=180^0-45^0-\left(\widehat{BAP}-\widehat{BAQ}\right)=180^0-45^0-45^0=90^0\)
\(\Rightarrow\)MP⊥AN tại P.
△MPN và △AHN có: \(\widehat{MPN}=\widehat{AHN}=90^0;\widehat{ANM}\) là góc chung.
\(\Rightarrow\)△MPN∼△AHN (g-g)
\(\Rightarrow\dfrac{AH}{MP}=\dfrac{AN}{MN};\dfrac{NP}{NH}=\dfrac{NM}{NA}\Rightarrow\dfrac{NP}{NM}=\dfrac{NH}{NA}\)
△APQ và △AMN có: \(\dfrac{NP}{NM}=\dfrac{NH}{NA};\widehat{MAN}\) là góc chung.
\(\Rightarrow\)△APQ∼△AMN (c-g-c)
\(\Rightarrow\dfrac{AQ}{AN}=\dfrac{PQ}{MN}\Rightarrow\dfrac{MN}{AN}=\dfrac{PQ}{AQ}\)
\(\dfrac{AH}{MP}=\dfrac{AN}{MN}\Rightarrow AH=MP.\dfrac{AN}{MN}=\dfrac{PQ}{AQ}.AB.\dfrac{AN}{AM}=AB\) không đổi.
Một bài đã làm không xong mà bạn ra hai bài thì ............
Bài 1: Con tham khảo tại câu dưới đây nhé.
Câu hỏi của Huyen Nguyen - Toán lớp 8 - Học toán với OnlineMath
Con tham khảo tại câu dưới đây nhé.
Câu hỏi của Huyen Nguyen - Toán lớp 8 - Học toán với OnlineMath
Áp dụng định nghĩa và giả thiết của hình vuông ABCD ta được:
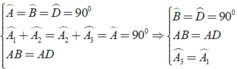
⇒ Δ ABM = Δ ADN( g - c - g )
Do đó AM = AN (cặp cạnh tương ứng bằng nhau)
* Trường hợp góc B nhọn:
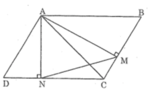
Xét △ AMB và △ AND, ta có:
∠ (AMB) = ∠ (AND) = 90 0
B = D (t/chất hình bình hành) ⇒ △ AMB đồng dạng △ AND (g.g)
Suy ra: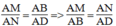 
Mà AD = BC (t/chất hình hình hành)
Suy ra: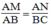 
Lại có: AB // CD (gt)
AN ⊥ CD (gt)
Suy ra: AN ⊥ AB hay ∠ (NAB) = 90 0
suy ra: ∠ NAM + ∠ MAB = 90 0 (1)
Trong tam giác vuông AMB ta có ∠ ABM = 90 0
Suy ra: ∠ (MAB) + ∠ B = 90 0 (2)
Từ (1) và (2) suy ra: ∠ NAM = ∠ B
Xét △ ABC và △ MAN ta có:
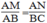(chứng minh trên)
∠ (NAM) = ∠ B (chứng minh trên)
Vậy △ ABC đồng dạng △ MAN (c.g.c)
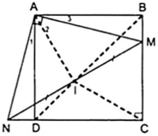
* Trường hợp góc B tù:
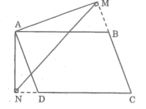
Xét △ MAN và △ AND, ta có:
∠ (AMB) = ∠ (AND) = 90 0
∠ (ABM) = ∠ (ADN) (vì cùng bằng C)
⇒ △ AMB đông dạng △ AND (g.g)
Suy ra: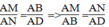
Mà AD = BC (t/chẩt hình bình hành)
Suy ra: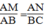 
Vì AB //CD nên ∠ (ABC) + ∠ C = 180 0 (3)
Tứ giác AMCN có ∠ (AMC) = ∠ (AND) = 90 0
Suy ra: ∠ (MAN) + ∠ C = 180 0 (4)
Từ (3) và (4) suy ra: (MAN) = (ABC)
Xét △ AMN và △ ABC, ta có:
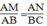(chứng minh trên)
∠ (MAN) = ∠ (ABC) (chứng minh trên)
Vậy △ MAN đồng dạng △ ABC (c.g.c)