Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Diện tích toàn phần của HLP là:
4 x 4 x 6 = 96 ( cm2)
Thể tích của HLP là:
4 x 4 x 4 = 64 ( cm3)
Đ/s: ..........
~ Hok T ~
S toàn phần là: 4 x 4 x6=96(cm2)
V là: 4 x 4 x 4=64(cm3)
sao lại là toán lớp 8????

Diện tích xung quanh là :
( 5 + 9 +5+ 9) * 8 = 224 ( cm2)
Diện tích 1 mặt đáy là :
5* 9 = 45 ( cm2)
Diện tích toàn phần là :
224 + 45 *2 = 314 (cm2)
ĐS : Sxq : 224 cm2
Stp : 314 cm2
OK

Tương tự 2A.
a) Hình chóp S.MNPQ là hình chóp đều vì các mặt bên là tam giác cân và đáy MNPQ là đa giác đều.
b)
V
'
V
=
1
6
. Chú ý 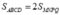

`V = 3x .4y . 2z= 24xyz`
Thay `x = 4 cm; y = 2cm; z= 1cm` ta có:
`24 . 4 . 2 . 1 = 192 cm^3`.
`S = 2 . (3x . 2z + 2z . 4y) = 2 . (6xz + 8zy) = 12xz + 16zy`
Thay `x = 4cm; y = 2cm; z = 1cm` ta có:
`12 . 4 . 1 + 16 . 1 . 2`
`= 48 + 32`
`= 80 cm^2`
Biểu thức biểu thị V của hình hộp chữ nhật là:
\(V=2z\cdot3x\cdot4y=24xyz\)
Biểu thức biểu thị S xung quanh của hình hộp chữ nhật là:
\(S_{xq}=\left(3x+4y\right)\cdot2\cdot2z=12xz+16yz\)
Thay \(x=4,y=2,z=1\) vào V và S ta có:
\(V=24\cdot4\cdot2\cdot1=192\left(cm^3\right)\)
\(S_{xq}=12\cdot4\cdot1+16\cdot2\cdot1=80\left(cm^2\right)\)

Chiều cao của hình HCN đó là:
`(6x^2y - 8xy^2) \div 2xy`
`= 6x^2y \div 2xy - 8xy^2 \div 2xy`
`= 3x - 4y`
Chiều cao là: `V : S = (6x^2y - 8xy^2) : 2xy = 3x - 4y`.

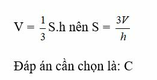

\(S_{tp}=6\cdot4^2=96\left(cm^2\right)\)
\(V=4^3=64\left(cm^3\right)\)
\(\Rightarrow B\)
Diện tích toàn phần hình lập phương:
$S_{tp}=6a^2=6.4^2=96(cm^2)$
Thể tích hình lập phương là:
$V=a^3=4^3=64(cm^3)$
$\to B$