
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


số bạn nam tình nguyện là x
số bạn nữ tình nguyện là y
tổng số bạn tình nguyện là x+y=49
số hộ gia đình các bạn tình nguyện là 5x+4y=5250 hộ
ta có pt:
\(\hept{\begin{cases}x+y=49\\5x+4y=5250\end{cases}}\)
\(\hept{\begin{cases}5x+5y=235\\5x+4y=5250\end{cases}< =>\hept{\begin{cases}y=-5015\\5x-25075=235\end{cases}}}\)(vô lí)
bạn xem lại đề bài nha số bạn nữ ra âm nên ko có no


Với n=0 \(\Rightarrow\) phương trình có 2 nghiệm duy nhất là \(\left\{{}\begin{matrix}x=-\dfrac{1}{2}\\y=\dfrac{1}{2}\end{matrix}\right.\)
Với n \(\ne0\)
Để phương trình có nghiệm duy nhất \(\Leftrightarrow\dfrac{n}{2}\ne\dfrac{2}{n}\Rightarrow n^2\ne4\Rightarrow n\ne\pm2\)
Vậy hệ phương trình có nghiệm duy nhất \(\forall n\ne\pm2\)
cho mình hỏi có đúng với nghiệm nguyên không vì đề bài yêu cầu nghiệm nguyên ạ ?

a, - Thay m = 2 vào phương trình ta được :\(x+2\sqrt{x-1}-3=0\)
\(\Leftrightarrow2\sqrt{x-1}=3-x\)
\(\Leftrightarrow4\left(x-1\right)=x^2-6x+9\left(x\le3\right)\)
\(\Leftrightarrow4x-4=x^2-6x+9\)
\(\Leftrightarrow x^2-10x+13=0\)
\(\Leftrightarrow\)\(x=5\pm2\sqrt{3}\) ( TM )
b, Ta có : \(x+2\sqrt{x-1}-m^2+6m-11=0\)
\(\Leftrightarrow x-1+2\sqrt{x-1}+1-m^2+6m-11=0\)
\(\Leftrightarrow\left(\sqrt{x-1}-1\right)^2=m^2-6m+9+2=\left(m-3\right)^2+2\)
\(\Leftrightarrow\sqrt{x-1}-1=\pm\sqrt{\left(m-3\right)^2+2}\)
\(\Leftrightarrow\sqrt{x-1}=1\pm\sqrt{\left(m-3\right)^2+2}\)
\(\Leftrightarrow x=\left(1\pm\sqrt{\left(m-3\right)^2+2}\right)^2+1\ge1\) ( TM )
=> ĐPCM
a) Thay \(m=2\) vào phương trình
\(\Rightarrow x+2\sqrt{x-1}-3=0\)
\(\Leftrightarrow2\sqrt{x-1}=3-x\) \(\left(3\ge x\ge1\right)\)
\(\Rightarrow4x-4=9-6x+x^2\)
\(\Leftrightarrow x^2-10x+13=0\) \(\Leftrightarrow\left[{}\begin{matrix}x=5+2\sqrt{3}\left(loại\right)\\x=5-2\sqrt{3}\end{matrix}\right.\)
Vậy ...
b) Đặt \(\sqrt{x-1}=a\) \(\left(a\ge0\right)\)
\(\Rightarrow a^2+2a-m^2+6m-10=0\)
Ta có: \(\Delta'=m^2-6m+11\ge0\forall m\)
Vậy phương trình luôn có nghiệm với mọi m

Ta có bài toán quen thuộc sau:
Nếu \(\left(x+\sqrt{x^2+1}\right)\left(y+\sqrt{y^2+1}\right)=1\) thì \(x+y=0\)
Do đó từ giả thiết ta chỉ cần chứng minh được \(\left(x+\sqrt{x^2+1}\right)\left(y+\sqrt{y^2+1}\right)=1\) thì bài toán được giải quyết.
Đặt \(\left\{{}\begin{matrix}x+\sqrt{x^2+1}=a>0\\y+\sqrt{y^2+1}=b>0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}\sqrt{x^2+1}=a-x\\\sqrt{y^2+1}=b-y\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x^2+1=a^2+x^2-2ax\\y^2+1=b^2+y^2-2by\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}2ax=a^2-1\\2by=b^2-1\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{a^2-1}{2a}\\y=\dfrac{b^2-1}{2b}\end{matrix}\right.\)
Thế vào giả thiết:
\(\left(\dfrac{a^2-1}{2a}+\sqrt{1+\left(\dfrac{b^2-1}{2b}\right)^2}\right)\left(\dfrac{b^2-1}{2b}+\sqrt{1+\left(\dfrac{a^2-1}{2a}\right)^2}\right)=1\)
\(\Leftrightarrow\left(\dfrac{a^2-1}{2a}+\sqrt{\dfrac{\left(b^2+1\right)^2}{\left(2b\right)^2}}\right)\left(\dfrac{b^2-1}{2b}+\sqrt{\dfrac{\left(a^2+1\right)^2}{\left(2a\right)^2}}\right)=1\)
\(\Leftrightarrow\left(\dfrac{a+b}{2}+\dfrac{a-b}{2ab}\right)\left(\dfrac{a+b}{2}-\dfrac{a-b}{2ab}\right)=1\)
\(\Leftrightarrow\left(\dfrac{a+b}{2}\right)^2-\left(\dfrac{a-b}{2ab}\right)^2=1\) (1)
Chú ý rằng: \(1=\dfrac{4ab}{4ab}=\dfrac{\left(a+b\right)^2-\left(a-b\right)^2}{4ab}\)
Do đó (1) tương đương:
\(\left(\dfrac{a+b}{2}\right)^2-\dfrac{\left(a-b\right)^2}{\left(2ab\right)^2}=\dfrac{\left(a+b\right)^2}{4ab}-\dfrac{\left(a-b\right)^2}{4ab}\)
\(\Leftrightarrow\dfrac{\left(a+b\right)^2}{4}\left(1-\dfrac{1}{ab}\right)+\dfrac{\left(a-b\right)^2}{4ab}\left(1-\dfrac{1}{ab}\right)=0\)
\(\Leftrightarrow\left[\dfrac{\left(a+b\right)^2}{4}+\dfrac{\left(a-b\right)^2}{4ab}\right]\left(1-\dfrac{1}{ab}\right)=0\)
Do \(a;b>0\Rightarrow\dfrac{\left(a+b\right)^2}{4}+\dfrac{\left(a-b\right)^2}{4ab}>0\)
\(\Rightarrow1-\dfrac{1}{ab}=0\Leftrightarrow ab=1\)
Hay \(\left(x+\sqrt{x^2+1}\right)\left(y+\sqrt{y^2+1}\right)=1\)
\(\Rightarrow x+y=0\Rightarrow P=100\)

C5:
\(A=\dfrac{a}{1+b^2c}+\dfrac{b}{1+c^2d}+\dfrac{c}{1+d^2a}+\dfrac{d}{1+a^2b}=\dfrac{a^2}{a+ab^2c}+\dfrac{b^2}{b+bc^2d}+\dfrac{c^2}{c+cd^2a}+\dfrac{d}{d+da^2b}\)
Áp dụng BĐT Cauchy Schwars dạng Engel ta có:
\(A\ge\dfrac{\left(a+b+c+d\right)^2}{a+b+c+d+ab^2c+bc^2d+cd^2a+da^2b}=\dfrac{16}{4+\left(ab+cd\right)\left(bc+ad\right)}\)
\(\ge\dfrac{16}{4+\left(\dfrac{ab+bc+cd+ad}{4}\right)^2}=\dfrac{16}{4+\left[\dfrac{\left(a+c\right)\left(b+d\right)}{2}\right]^2}\ge\dfrac{16}{4+\left[\dfrac{\left(\dfrac{a+b+c+d}{2}\right)^2}{2}\right]^2}=2\)
Dấu ''='' xảy ra khi và chỉ khi a=b=c=d=1

Lời giải:
ĐK:.............
Đặt $\sqrt{2x^2+x+6}=a; \sqrt{x^2+x+2}=b$ với $a,b\geq 0$ thì PT trở thành:
$a+b=\frac{a^2-b^2}{x}$
$\Leftrightarrow (a+b)(\frac{a-b}{x}-1)=0$
Nếu $a+b=0$ thì do $a,b\geq 0$ nên $a=b=0$
$\Leftrightarrow \sqrt{2x^2+x+6}=\sqrt{x^2+x+2}=0$ (vô lý)
Nếu $\frac{a-b}{x}-1=0$
$\Leftrightarrow a-b=x$
$\Leftrightarrow \sqrt{2x^2+x+6}=\sqrt{x^2+x+2}+x$
$\Rightarrow 2x^2+x+6=2x^2+x+2+2x\sqrt{x^2+x+2}$ (bình phương 2 vế)
$\Leftrightarrow 2=x\sqrt{x^2+x+2}(1)$
$\Rightarrow 4=x^2(x^2+x+2)$
$\Leftrightarrow x^4+x^3+2x^2-4=0$
$\Leftrightarrow (x-1)(x^3+2x^2+4x+4)=0$
Từ $(1)$ ta có $x>0$. Do đó $x^3+2x^2+4x+4>0$ nên $x-1=0$
$\Rightarrow x=1$Vậy..........
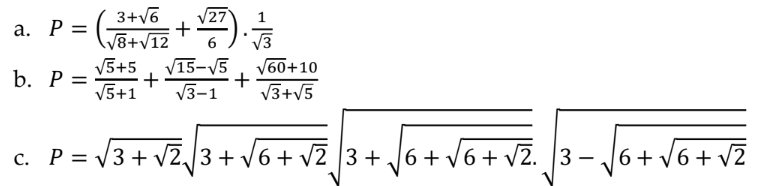





a: \(=\left(\dfrac{\sqrt{3}}{2}+\dfrac{\sqrt{3}}{2}\right)\cdot\dfrac{1}{\sqrt{3}}=\sqrt{3}\cdot\dfrac{1}{\sqrt{3}}=1\)
b: \(=\sqrt{5}+\sqrt{5}+2\sqrt{5}=4\sqrt{5}\)
c: \(=\sqrt{3+\sqrt{2}}\cdot\sqrt{3+\sqrt{6+\sqrt{2}}}\sqrt{9-6-\sqrt{6+\sqrt{2}}}\)
\(=\sqrt{3+\sqrt{2}}\cdot\sqrt{3+\sqrt{6+\sqrt{2}}}\cdot\sqrt{3-\sqrt{6+\sqrt{2}}}\)
=căn 3+căn 2*căn 3-căn 2
=căn 9-2=căn 7