NH
6
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
P
0
QT
1
19 tháng 9 2023
Vì \(\Delta ABC\) đều nên AB = AC = BC (tính chất tam giác đều)
Vì I là điểm cách đều 3 cạnh của tam giác nên là giao điểm của 3 đường phân giác của tam giác ABC
Áp dụng ví dụ 2, ta được, AI là đường trung tuyến của \(\Delta ABC\)
Tương tự, ta cũng được BI, CI là đường trung tuyến của \(\Delta ABC\)
Vậy I là giao điểm của ba đường đường trung tuyến của \(\Delta ABC\) nên I là trọng tâm của \(\Delta ABC\).
Chú ý:
Với tam giác đều, giao điểm của 3 đường trung tuyến cũng là giao điểm của 3 đường phân giác.
NB
1
LY
7 tháng 4 2017
Bạn biết rằng đường trung tuyến của tam giác đều cũng là đường phân giác của tam giác
Mà <A = <B = <C ( dấu góc đó nhe bạn, mình k bik bấm dấu góc ở đâu hết :) )
=> <A / 2 = <B / 2 = <C / 2
=> <A1 = <A2 = <B1 = <B2 = <C1 = <C2
Xét tam giác AHC có: <A1 = <C1 => tam giác AHC là tam giác cân tại H => AH = HC (1)
Xét tam giác HCB có: <C1 = <B2 => tam giác BHC là tam giác cân tại H => HC = HB (2)
Xét tam giác BHA có: <B2 = <A2 => tam giác BHA là tam giác cân tại H => HB = HA (3)
Từ (1), (2), (3) => HA = HB = HC => điều phải chứng minh
19 tháng 4 2017
a) - Trọng tâm của một tam giác có tính chất như sau:
"Trọng tâm cách đỉnh một khoảng bằng 2/3 độ dài đường trung tuyến đi qua đỉnh đó."
- Các cách xác định trọng tâm:
+ Cách 1: Vẽ hai đường trung tuyến ứng với hai cạnh tùy ý, rồi xác định giao điểm của hai đường trung tuyến đó.
+ Cách 2: Vẽ một đường trung tuyến của tam giác. Chia độ dài đường trung tuyến thành ba phần bằng nhau rồi xác định một điểm cách đỉnh hai phần bằng nhau.
b) Không thể vẽ được một tam giác có trọng tâm ở bên ngoài tam giác vì đường trung tuyến qua một đỉnh của tam giác và trung điểm một cạnh trong tam giác nên đường trung tuyến phải nằm giữa hai cạnh của một tam giác tức nằm ở bên trong của một tam giác nên ba đường trung tuyến cắt nhau chỉ có thể nằm bên trong của tam giác.
19 tháng 4 2017
Trả lời
a) - Trọng tâm của một tam giác có tính chất như sau:
"Trọng tâm cách đỉnh một khoảng bằng 2/3 độ dài đường trung tuyến đi qua đỉnh đó."
- Các cách xác định trọng tâm:
+ Cách 1: Vẽ hai đường trung tuyến ứng với hai cạnh tùy ý, rồi xác định giao điểm của hai đường trung tuyến đó.
+ Cách 2: Vẽ một đường trung tuyến của tam giác. Chia độ dài đường trung tuyến thành ba phần bằng nhau rồi xác định một điểm cách đỉnh hai phần bằng nhau.
b) Không thể vẽ được một tam giác có trọng tâm ở bên ngoài tam giác vì đường trung tuyến qua một đỉnh của tam giác và trung điểm một cạnh trong tam giác nên đường trung tuyến phải nằm giữa hai cạnh của một tam giác tức nằm ở bên trong của một tam giác nên ba đường trung tuyến cắt nhau chỉ có thể nằm bên trong của tam giác.
QT
1
19 tháng 9 2023
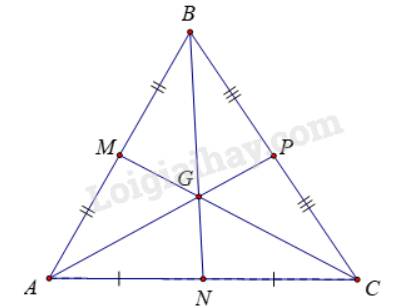
Tam giác ABC đều nên AB = BC = CA
Tam giác ABC cân tại B có BN là đường trung tuyến
\( \Rightarrow BN\)là đường trung trực của đoạn thẳng AC
Tam giác BAC cân tại A có AP là đường trung tuyến
\( \Rightarrow AP\)là đường trung trực của đoạn thẳng BC
Mà \(BN \cap AP = G\)
\( \Rightarrow G\)là giao điểm ba đường trung trực của tam giác ABC
\( \Rightarrow GA = GB = GC\).
1. Chứng minh G là giao điểm của hai đường trung tuyến trong tam giác.
2. Chứng minh G thuộc trung tuyến và chia trung tuyến theo tỉ lệ 2 : 1.
Tích nha
Học tốt
Bạn Cho mình 1 vd được ko